4

The title of this post is intentionally sensational, but what I am really going to do is to compare the divergent integrals $\int_0^1\frac1xdx$ and $\int_1^\infty\frac1xdx$.

Let's consider the transform $\mathcal{L}_t[t f(t)](x)$. It is notable by the fact that it preserves the area under the curve: $$\int_0^\infty f(x)dx=\int_0^\infty \mathcal{L}_t[t f(t)](x) dx$$

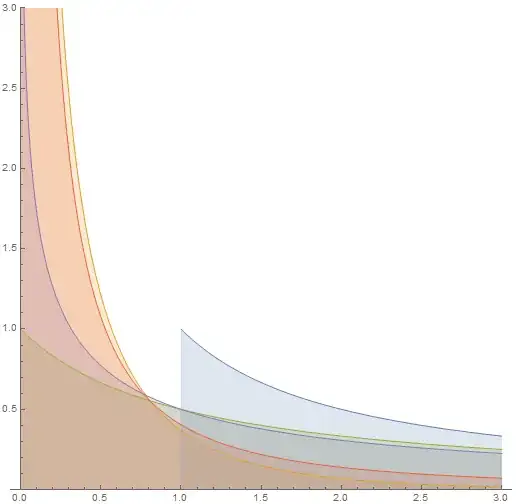
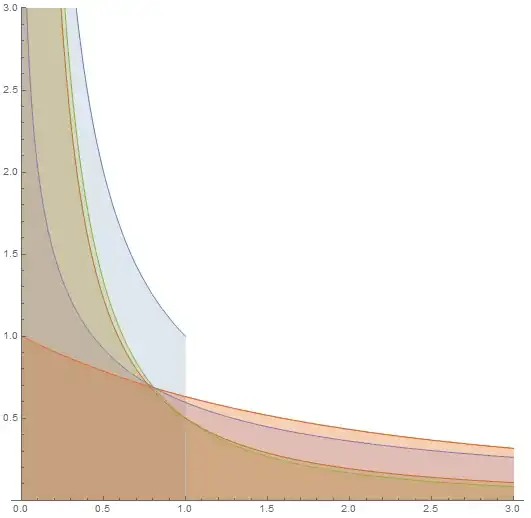
But more interesting, it also works well with divergent integrals, allowing us to define the equivalence classes of divergent integrals. Particularly, by successfully applying this transform to $\int_1^\infty \frac1xdx=\int_0^\infty\frac{\theta (x-1)}{x}dx$, one can obtain the following equivalence class of divergent integrals (the first one and the third one turn out to be similar up to a shift):

$\int_0^\infty\frac{\theta (x-1)}{x}dx=\int_0^\infty\frac{e^{-x}}{x}dx=\int_0^\infty\frac{dx}{x+1}=\int_0^\infty\frac{e^x x \text{Ei}(-x)+1}{x}dx=\int_0^\infty\frac{x-\ln x-1}{(x-1)^2}dx$

enter image description here

On the other hand, applying the transform to $\int_0^1\frac1x dx=\int_0^\infty \frac{\theta (1-x)}{x}dx$ one can obtain another set of equal integrals:

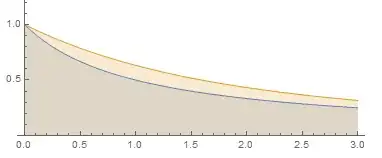
$\int_0^\infty\frac{\theta (1-x)}{x}dx=\int_0^\infty\frac{1-e^{-x}}{x}dx=\int_0^\infty\frac{1}{x^2+x}dx=\int_0^\infty-e^x \text{Ei}(-x)dx=\int_0^\infty-\frac{x-x\ln x-1}{(x-1)^2 x}dx$ enter image description here

Now, having postulated equivalence of divergent integrals in each class, we can pick two integrals, one from each class and compare them. Well, it seems, the integrals in the second class are bigger by an Euler's constant:

$\int_0^{\infty } \left(\frac{1-e^{-x}}{x}-\frac{1}{x+1}\right) \, dx=\gamma$

enter image description here

And thus, we can conclude that $\int_0^1\frac1xdx=\gamma+\int_1^\infty \frac1xdx$. Surprising, is not it, given that one would naively expect $\ln 0=-\ln\infty$?

But we also have an identity $\gamma = \lim_{n\to\infty}\left(\sum_{k=1}^n \frac1{k}-\int_1^n\frac1t dt\right)$ and know the regularized value of harmonic series $\operatorname{reg}\sum_{k=1}^n \frac1{k}=\gamma$. Thus, we obtain $$\int_0^1\frac1xdx=\gamma+\int_1^\infty\frac1xdx=\sum_{k=1}^\infty\frac1k.$$

So, the integrals differ by Euler-Mascheroni constant. Is there any logical explanation for this?

Anixx
  • 10,161
  • 1
    I would ask what exactly is the "equivalence of the divergent integrals". From the symmetry it seems to be obvious that $\int_0^1\frac{dx}x-\int_1^\infty\frac{dx}x=1$. – user Mar 25 '21 at 10:26
  • @user yes, from the symmetry one can make this conclusion as well. But if we trust that this Laplace-based transform keeps for divergent integrals as well (and from other areas we know that $\int_0^\infty \frac1{x^2}dx=\int_0^\infty dx$, which is supported by this transform really works)? the result is different. – Anixx Mar 25 '21 at 10:28
  • But $1\ne\gamma$ as you see. I would assume we deal here with a similar phenomenon as by the summation of not absolutely convergent series. One can at will obtain almost any result. – user Mar 25 '21 at 10:32
  • @user symmetry between the axes consideration does not work for divergent integrals at all: $\int_0^\infty (2x-x)dx$ and $\int_0^\infty (x-1/2 x)dx$ are symmetric but their growth rate is different (the former is twice the later). If you swap the axes, you will obtain the opposite result. – Anixx Mar 25 '21 at 10:34
  • @user so, divergent integral is not the same as area of a figure, because it can change if you change the axes along which you integrate. – Anixx Mar 25 '21 at 10:35
  • You have put forward the argument with conserved area, therefore I took this example. – user Mar 25 '21 at 10:41
  • @user what do you mean? My argument is that divergent integrals are NOT the same as areas because area does not change if you change the axes along which you integrate, shift a figure or change filtering, while divergent integrals can change under all there rearrangements. For instance, integrals $\int_0^\infty1dx$ and $\int_1^\infty 1 dx$ differ by $1$, while the figures under the plot are different only by a shift. – Anixx Mar 25 '21 at 10:44

1 Answers1

1

Why is $\ln 0\ne-\ln \infty$?

They are equal: $\ln 0 = -\infty$ and $-\ln \infty = -\infty$.

And thus, we can conclude that $\int_0^1\frac1xdx=\gamma+\int_1^\infty \frac1xdx$. Surprising, is not it, given that one would naively expect $\ln 0=-\ln\infty$?

Not at all. $$-\infty = \gamma - \infty.$$ You see, $\infty$ is infinite. And this sort of thing is exactly what makes "infinite" different from "finite".

And per user's comments, it is also true that $-\infty = 1 - \infty$. That too is part of infinity's shtick.

There is no logical inconsistency here. The only problem is that you are trying to enforce intuition developed from finite behavior on infinite behavior where it does not hold.

If infinity didn't behave like this, we would have just added it to the real numbers, just like we added $0$ and negative numbers in the past, and even added a square root of $-1$, though for that one we were at least willing to admit the result deserved its own separate name.

But we don't add $\infty$ to the real numbers, and even tell people that "infinity doesn't exist" for years, as if we couldn't just define it, exactly because it doesn't play well with other numbers. And it is more of pain to deal with all the exceptional behavior than it is to just kick infinity out of the playground.

Only after someone develops the mathematical chops to recognize how it needs to be handled do we admit to them that yes, infinity does exist after all.

Paul Sinclair
  • 45,932