1

First of all: I searched with different search engines and on StackExchange, but did not find a solution to my problem. This may be because its specific description is kind of long. For the same reason, I had to choose an unspecific title to this question due to the character limit.

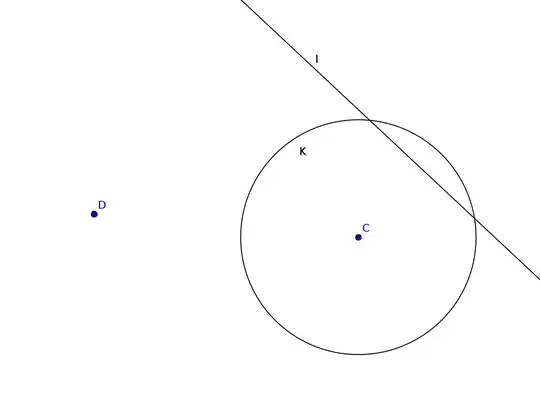
Now, here is my problem: Given

  • A point $D$
  • A line $l$
  • A circle $K$ (with center $C$ and radius $r$)

all in $\mathbb{R}^2$ Problem setting

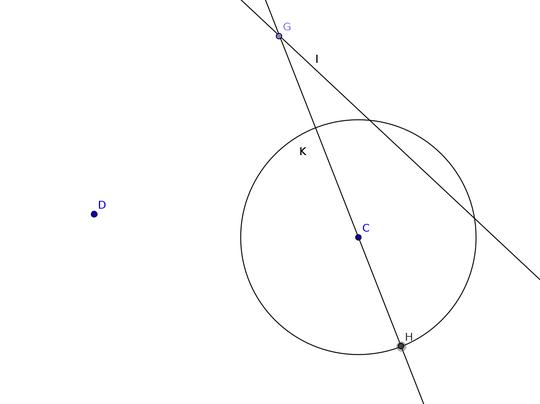
I want to find a point $G$ such that:

  • $G$ is incident to $l$
  • Let the intersection of the line $GC$ with $K$ be $H$. It should hold that $G$ has the same distance to $D$ as to $H$, i.e. $\left\lVert\vec{GD}\right\rVert = \left\lVert\vec{GH}\right\rVert$ enter image description here

So far I tried to find some property that this point has that allows me to construct it, but haven't found one yet. I am also very inexperienced and have little to no knowledge in geometry, which might be why this is hard to me.

Edit (clarifications):

  • $D$ and $C$ may be assumed to lie on the same side of $l$ (I guess this can even be assumed w.l.o.g., as we could otherwise just mirror the point $D$).
  • $H$ is the intersection point that is further away from $G$ than $C$.
  • $D$ can be assumed to be exterior $K$.
  • $l$ can be assumed to intersect $K$ at two different points and to not pass through $C$.
  • I preferably look for geometric solutions or algebraic solutions in closed form.
Jakob E.
  • 915
  • Can we assume that $D$ is exterior $K$? That $ell$ intersects $K$ but doesn't pass through $C$? That $D$ and $C$ are both on the same side of $\ell$? Also, $GC$ intersects $K$ in two points. Is it required that $G$ and $H$ be on opposite sides of $C$? I don't know which, if any, of these points are important, but diagrams can be misleading. – saulspatz Mar 20 '21 at 18:50

2 Answers2

5

  1. Reflect $D$ in the line $l$, denote the image $D^*$.

  2. Draw the line $DD^*$.

  3. Pick an arbitrary, but convenient, point $E$ on the line $l$ and draw the circle with center $E$ and radius $ED = ED^*$. It is very helpful if this circle $K(E, ED)$ intersects the the original one $K$ at two points.

  4. Draw the radical axis of the two circles $K(E, ED)$ and $K$. If the two circle intersect, then the radical axis is the line that passes through both intersection points of the two circles.

  5. Denote by $F$ the intersection point between the radical axis and the line $DD^*$

  6. Construct the line through point $F$ and tangent to the circle $K$. There are two of them, so you have two solutions.

  7. Denote by $T$ the point of tangency between the line from point 5 and the circle $K$.

  8. The circumcircle of triangle $\Delta \, TDD^*$ is the circle you are looking for (there are two solutions).

Futurologist
  • 9,659
  • Thank you very much for the detailed and simple instructions! In step 4, I think you mean $K(E,ED)$. – Jakob E. Mar 21 '21 at 15:10
  • 1
    @JakobW. Yes, you are right, I had a typo. Now it's fixed. Cheers! – Futurologist Mar 21 '21 at 15:12
  • @Futurologist This elegant construction also answers the problem: "To determine the points in which a given straight line intersects a conic of given focus, directrix and eccentricity." See my answer: https://math.stackexchange.com/questions/4185613/given-the-two-foci-and-the-vertices-of-an-hyperbola-and-a-random-line-how-can-on. Also compare with the construction given by Charles Taylor on p. 10-11 in "An introduction to the Ancient and Modern Geometry of Conics" 1881. A pdf is available somewhere on the web. – Arne Erikson Nov 05 '23 at 07:13
1

Sketch for an algebraic solution.

Translate, rotate and scale your picture so that the circle is the unit circle, the line $\ell$ is horizontal at known height $y=h$. Then $D$ will have known coordinates $(c,d)$. The distance from $D$ to $\ell$ is $d-h$. Suppose $G=(x,h)$. Then the line from $G$ through the center of the circle has meets the circle at the two points $\theta$ for which $b/a = \tan(\theta)$. Moreover, $G = ((\tan \theta)/h, h)$.

Equate the squares of the two distances you care about: $$ (c- ((\tan \theta) / h)^2 + (d- h)^2= (a-\cos \theta)^2 + ( b - \sin \theta)^2 $$

That's sufficient information to solve for the angle $\theta$. You may encounter algebraic problems that will reflect the fact that the ambiguities in the picture suggest cases with no solutions and multiple solutions.

Ethan Bolker
  • 103,433
  • If I try to solve this equation, I get something like $\cos \theta + \sin \theta = \text{some constant}$. Do you know how I could proceed from there? – Jakob E. Mar 20 '21 at 19:06
  • I suspect there is no closed form solution so you will need numerical methods. Note: I edited to match the question. In the old version I used the distance from $D$ to $\ell$ instead of the distance to $G$. You should check my trigonometry. – Ethan Bolker Mar 20 '21 at 19:35