0

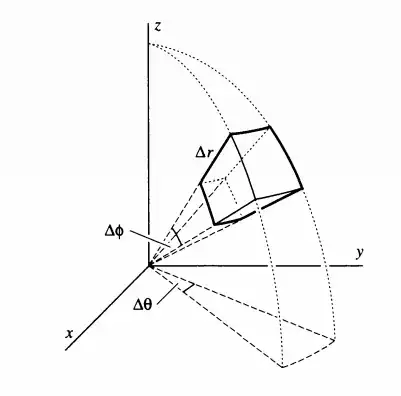
I am trying to derive the divergence operator in spherical coordinates using the 'cuboid' volume method, which is used in the book Div, Grad, Curl and All That by Schey, Problem II 21.

See: Using Cylindrical Coordinates to Compute Curl gradient and divergence using coordinate free del definition in cylindrical coordinate

I used the volume element $\Delta V = \Delta r (r \Delta \phi) (r \Delta \theta) = r^2 \Delta r \Delta \phi \Delta \theta$

($\theta$ is the azimuthal angle)

However, the result I got is the divergence operator in spherical coordinates without the $\sin \phi$.

What is the correct volume?

P.S. it seems $\Delta V = \Delta r (r \Delta \phi) (r \sin\phi \Delta \theta) = r^2 \sin\phi \Delta r \Delta \phi \Delta \theta$ is correct. But why?

Edit: I think I found out why? $r \sin\phi$ is the projection of the radius 'vector' on the x-y plane, and $r \sin\phi \Delta \theta$ is the length of the arc swept across by $\Delta \theta$ (or rather approximately)?

Volume element

Cheng
  • 299

1 Answers1

2

The answer you gave yourself in your edit is correct :)

It is not really a PROOF in the strict sense, because how do you know that approximation is sufficient? But in some ways it is better than a proof, because it gives you a good intuition of where the volume element comes from. It turns out that when $\Delta r,\Delta \phi,\Delta\theta$ are made small enough, the result limits to the right value using the approximation that the region has the shape of a rectangular prism.

spinachflakes
  • 945