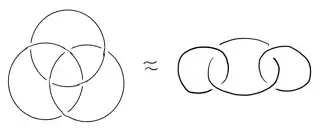Let's start by fixing some notation. The ordered configuration space of three distinct points in $\mathbb{C}$ is
$$\operatorname{OConf}^3(\mathbb{C})=\mathbb{C}^3-\Delta^3\mathbb{C}$$
where $\Delta^3\mathbb{C}=\{(z_1,z_2,z_3)\in\mathbb{C}^3\mid \exists i\neq j, z_i=z_j\}$, the fat diagonal. Another way to write the fat diagonal is as the zero set of a polynomial. Anticipating discriminants, we'll use $(z_1-z_2)^2(z_1-z_3)^2(z_2-z_3)^2$.
The symmetric group $S_3$ acts on $\mathbb{C}^3$ by permutation of coordinates, and furthermore it acts on $\Delta^3\mathbb{C}$. Hence, $S_3$ acts on $\operatorname{OConf}^3(\mathbb{C})$. It does so in a properly discontinuous way, and thus the quotient yields a space $\operatorname{Conf}^3(\mathbb{C})$ covered by $\operatorname{OConf}^3(\mathbb{C})$. This is a six-fold normal cover (in particular, a principal $S_3$-bundle).
The $S^3$ action on $\mathbb{C}^3$ is linear, and it splits as a direct sum $\mathbb{C}^3=V_1\oplus V_2$ where $V_1$ is spanned by $(1,1,1)$ and $V_2$ is the orthogonal complement, the set of $(z_1,z_2,z_3)$ such that $z_1+z_2+z_3=0$. Define $\operatorname{OConf}^3_0(\mathbb{C})=V_2-\Delta^3\mathbb{C}$ to be the reduced ordered configuration space. There is a deformation retract from $\operatorname{OConf}^3(\mathbb{C})$ to $\operatorname{OConf}^3_0(\mathbb{C})$ by collapsing $V_1$ to a point, so at least homotopically this reduced space is "the same." This deformation retract respects the $S_3$ action hence yields a quotient space $\operatorname{Conf}^3_0(\mathbb{C})$. Just to reiterate, these reduced configuration spaces are of triples of points whose sum is 0 -- what we did was remove a homotopically uninteresting translation symmetry ($V_1$).
There is another homotopically uninteresting symmetry to $\operatorname{OConf}^3_0(\mathbb{C})$, which is scaling a configuration by a positive real number. That is, $(z_1,z_2,z_3)$ and $(rz_1,rz_2,rz_3)$ for $r\in\mathbb{R}_{>0}$ are essentially the same when $z_1+z_2+z_3=0$. We can consider the intersection of $\operatorname{OConf}^3_0(\mathbb{C})$ with a sphere in $V_2$ centered at the origin, which has the effect of choosing some representative scaling for each triple. Another description of this intersection is taking the complement of a link of the singularity at $0$ of $(z_1-z_2)^2(z_1-z_3)^2(z_2-z_3)^2$ restricted to $V_2$.
Consider the following orthonormal basis for $V_2$:
$$\left\{
\frac{1}{\sqrt{2}}\begin{bmatrix}
1\\-1\\0
\end{bmatrix},
\frac{1}{\sqrt{6}}\begin{bmatrix}
1\\1\\-2
\end{bmatrix}
\right\}$$
Using $(x,y)$ coordinates with respect to this basis, we have
$$(z_1-z_2)^2(z_1-z_3)^2(z_2-z_3)^2 = \tfrac{1}{2}x^2(x-\sqrt{3}y)^2(x+\sqrt{3}y)^2.$$
Let's check that the link of this singularity is a 3-component Hopf link. The $S^3$ under consideration is the set of $(x,y)\in\mathbb{C}^3$ such that $\lVert x\rVert^2+\lVert y\rVert^2=1$, and in $\mathbb{C}^2$ the zero set is clearly the three complex lines respectively given by the equations $x=0$, $x=\sqrt{3}y$, and $x=-\sqrt{3}y$. The intersection of a complex line with $S^3$ is a fiber of the Hopf fibration, so we've identified it. But, for sake of making pictures, we can plot a stereographic projection just to be sure:

Mathematica:
stereo[a_, b_] := {Im[a], Re[b], Im[b]}/(1 - Re[a]);
components = {stereo[0, E^(I t)],
stereo[Sqrt[3]/2 E^(I t), 1/2 E^(I t)],
stereo[Sqrt[3]/2 E^(I t), -(1/2) E^(I t)]};
ParametricPlot3D[components, {t, 0, 2 Pi}, Axes -> False,
Boxed -> False] /. Line[pts_] :> Tube[pts, 0.1]
Now let's see how generators of $S_3$ act on $S^3$. The first generator we'll consider is $\tau(z_1,z_2,z_3)=(z_2,z_1,z_3)$, given in the original $\mathbb{C}^3$ coordinates. In $(x,y)$ coordinates, this is $\tau(x,y)=(-x,y)$. Something we can deduce right now is that this transformation will leave the first component of the link fixed while swapping the other two components.
To visualize this, there is a family of transformations $\tau_t(x,y)=(e^{\pi i t}x,y)$ for $0\leq t\leq 2$ with $\tau_1=\tau$ and $\tau_0=\tau_2=\operatorname{id}$. Here's a first animation involving the same stereographic projection from before:

It is somewhat misleading because there's an ambiguity with the axis of rotation: the axis of rotation is the first component! This can be made clearer using a stereographic projection where one of the points of the first component goes to infinity:
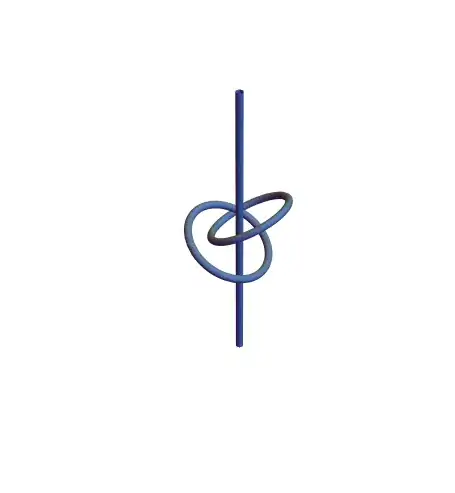
From this point of view $\tau$ is a rotation by 180 degrees about the vertical axis.
Let's now look at the second generator, $\sigma(z_1,z_2,z_3)=(z_2,z_3,z_1)$. In $(x,y)$ coordinates, this is $$\sigma(x,y)=(-\tfrac{1}{2}x+\tfrac{\sqrt{3}}{2}y,-\tfrac{\sqrt{3}}{2}x-\tfrac{1}{2}y),$$
which when restricted to $\mathbb{R}^2$ is a rotation by 120 degrees about the origin. Evidently, this does a cyclic permutation of the three components. We can visualize this transformation by a family of transformations given by rotations through various angles:
$$\sigma_\theta(x,y)=(\cos(\theta)x+\sin(\theta)y,-\sin(\theta)x+\cos(\theta)y)$$
where $\sigma_{2\pi/3}=\sigma$. Using the first stereographic projection, we get this animation:

And using the second stereographic projection for comparison:

Recall that the isometry group of $S^3$ is $SO(4)$. The matrix of $\sigma$ in the basis $\{(1,0),(0,1),(i,0),(0,i)\}$ is block diagonal with two $2\times 2$ rotations by 120 degrees clockwise. Thinking of $\sigma$ as being the composition of these two commuting rotations (from setting one of the two blocks to the identity matrix), then we see that $\sigma$ is a composition of two rotations about geodesics. One on the plane spanned by the first two vectors (parameterized by $(x,y)=(\cos t,\sin t)$) and the second on the plane by the last two (parameterized by $(x,y)=(i\cos t,i\sin t)$). Plotting those axes should make it more clear:

After a small rotation, we can put those rotation axes into the "standard" 2-component Hopf link position:

There is another way to visualize this. The 3-components of the link lie on a Clifford torus, and we can stereographically project in such a way that this torus is "standard." The torus can be parameterized by $(x,y)=(\sin(\theta)e^{i t},\cos(\theta)e^{i t})$ where the three components of the link are given by $\theta=0,-2\pi/3,2\pi/3$. Putting some red beads on the components to be able to keep track of the rotations, we see this:
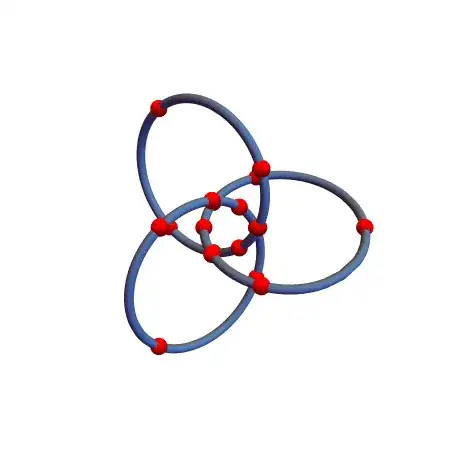
(One application of $\sigma$ corresponds to a component rotating two components counter-clockwise.)
Note: this section is not complete and goes beyond the original question. I want to eventually work out how to see the branched cover $S^3\to S^3$ with a trefoil branch locus dircetly.
A way to encode points of $\operatorname{Conf}^3_0(\mathbb{C})$ is via cubic polynomials by
$$[(z_1,z_2,z_3)]\mapsto (z-z_1)(z-z_2)(z-z_3).$$
This certainly respects the $S_3$ action so it is well-defined. The roots of this polynomial recover the original triple (up to permutation by $S_3$).
Since $z_1+z_2+z_3=0$, then we have
$$(z-z_1)(z-z_2)(z-z_3) = z^3+(z_1z_2+z_1z_3+z_2z_3)z-z_1z_2z_3$$
and thus the map $(z_1,z_2,z_3)\mapsto (z_1z_2+z_1z_3+z_2z_3, z_1z_2z_3)$ identifies the space of unordered triples (allowing multiplicities) with $\mathbb{C}^2$. In fact, we get an orbifold cover $V_2\to \mathbb{C}^2$ this way. Our goal is to take the $S^3\subset V_2$ and show the image in $\mathbb{C}^2$ is another $S^3$, and then say that this gives a six-fold branched cover $S^3\to S^3$ with a trefoil branch locus, whose preimage in $S^3$ is the 3-component Hopf link.
Setting $e_2=z_1z_2+z_1z_3+z_2z_3$ and $e_3=z_1z_2z_3$, it is worth computing the image of $\Delta^3\mathbb{C}$ in $(e_2,e_3)$ coordinates. It turns out that when $z_1+z_2+z_3=0$ then
$$(z_1-z_2)^2(z_1-z_3)^2(z_2-z_3)^2=-4e_2^3-27e_3^2.$$
This is the discriminant of the cubic polynomial $z^3+e_2z-e_3$.
In the $(x,y)$ basis, we can compute that
$$(e_2,e_3) = \left(-\tfrac{1}{2}(x^2+y^2), -\tfrac{1}{3\sqrt{6}}y(y-\sqrt{3}x)(y+\sqrt{3}x)\right)$$
(and one can verify this is invariant under $\tau$ and $\sigma$, as expected).
Unfortunately, $S^3$ doesn't map to anything that's obviously spherical, so I'll stop here for now. At least, it's not so hard to work out that the link of the singularity $-4e_2^3-27e_3^2=0$ is a trefoil knot in $(e_1,e_2)$ coordinates.
By the way, this six-fold cover of the trefoil exterior is "Narnia" from the video Knots to Narnia with Bill Thurston. The cover is associated to a homomorphism $\pi_1(S^3-3_1)\to S_3$, and one can check that by imposing the relation that a meridian squared is the identity (what I've heard called the "meridianal rank-2 knot group") that one gets a group isomorphic to $S_3$, hence there is a unique $S_3$ cover. In particular, with the presentation $\langle a,b\mid aba=bab,a^2=1\rangle$ one can check that $b^2=1$ as well and so this is the $A_2$ Coxeter group, hence $S_3$.
For fun, here's a gif showing the motion of the roots of polynomials when taking a meridian path around the trefoil. Each loop around swaps the two roots to the right, and so going around a meridian twice returns the roots to their original positions.
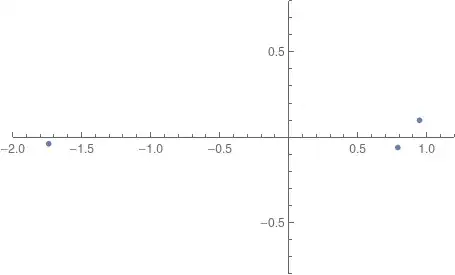
This gives some intuition for the branched cover -- the branch locus corresponds to when the polynomial has a root of multiplicity 2.