Preamble
Whenever all the variables under consideration are expressed in the same unit of measurement and therefore they appear to be directly comparable, the Euclidean scalar product or the associated Euclidean distance is usually used,
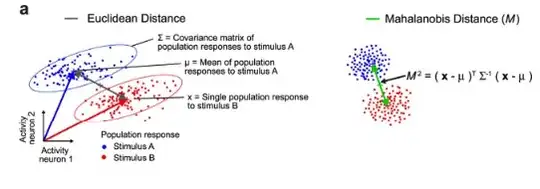
$ d^2(\mu,x)\equiv \langle \mu - x,\mu - x \rangle_{eucl}:= \sum_{i=1}^n (\mu_i - x_i)^2 $
Often, the collected data do not have homogeneous units of measurement, for example in the pair of weight-height variables, the unit of measurement of the first variable is mass, while the second variable expresses the measurement of a length. Weight and height cannot be added together, so it is necessary to express the data in dimensionless numbers. If the variables refer to different units of measurement, the Weighted Euclidean Distance is used in order to transforms the observable variables into dimensionless and therefore comparable numbers.The transformation is operated by a suitable multiplier or weight, $\lambda_i$, which makes the observed difference $(\mu_i - x_i)$ of a character directly comparable with the observed difference in one of the other characters $(\mu_j - x_j)$ where $i\neq j$ and $i,j=1,\cdots, n$.
If the measurements of the single variables have non-univocal values, i.e. in probabilistic terms they present non-zero variance, it is common to choose the reciprocal of the standard deviation as the multiplier: $\lambda = 1 / \sigma $ (Mahalanobis transformation), where $\sigma $ designates the standard deviation.
The Mahalanobis transformation that operates on vectors by multiplying them by the reciprocal of the corresponding standard deviation $ x \mapsto f (x):= \sigma^{-1}x$ is an isometry with respect to the usual Euclidean scalar product:
$\langle\mu - x,\mu - x\rangle_{mahal} = \langle f(\mu - x),f(\mu - x)\rangle_{eucl}$
If the n variables are statistically independent, therefore uncorrelated, the square of the Mahalanobis distance is written as:
$d^2(\mu - x,\mu - x)_{mahal}:= \sum_{i=1}^n \tfrac{(\mu_i - x_i)^2} {\sigma^2_{ii}} $
where $\sigma^2_{ii}$ is the variance referred to the i-th variable.
Otherwise, if the n variables are correlated, the square of the Mahalanobis distance is written as
$d^2(\mu - x,\mu - x)_{mahal}:= \sum_{i=1}^n \sum_{j=1}^n (\mu_i - x_i) \cdot \sigma^{-2}_{ij} \cdot (\mu_j - x_j) $,
where $\sigma^{2}_{ij} $ is the element of the inverse matrix of the variance-covariance matrix $\Sigma$.
In short
- $M=(\mu - x)^t \Sigma^{-1} (\mu - x) $
Question 1
Once a distance $d$ able to express the notion of proximity for the observations has been adopted, it is possible to introduce a classification rule for the observations with respect to a representative of each class. The statistical character of the discriminant analysis derives from the fact that the average or the sample mean of the populations under examination is chosen to be the representative of each class.
In the example of the two classes (sets "US" and "CS"), indicated with $ \mu_1$ the average of the first set (population) and with $ \mu_2$ the average of the second population, the observation $x$ belongs to class 1 if and only if:
- $d(\mu_1,x) < d(\mu_2,x)$
that is if $x$ is closer to $\mu_1$.
Question 2
Just consider $d^2(\mu,x)=\|\mu-x\|^2=\langle \mu-x , \mu-x \rangle$ to express the rule of belonging to set 1 in terms of the dot product as
$\langle \mu_1-x, \mu_1-x\rangle < \langle \mu_2-x, \mu_2-x\rangle$
The relationship just written, exploiting the bilinearity property of the scalar product, can be rewritten after simple steps such as
$\langle \mu_1-\mu_2, x-1/2(\mu_1+\mu_2)\rangle > 0$.
Indicated with $x_0=1/2(\mu_1+\mu_2)$ the classification rule for set 1 elements becomes:
- $Set_1: \langle \mu_1-\mu_2, x-x_0 \rangle > 0 $