3

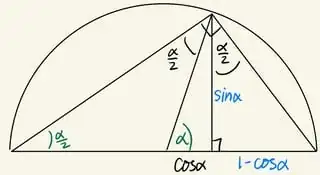
Is it true that

$$\bbox[5px,border:2px solid #138D75]{\tan\left(\frac {\alpha}2\right)=\frac{1-\cos\alpha}{\sin \alpha}, \quad ?} \tag1$$

My solution: First, we note that the expression $\tan \left ( \frac{\alpha}{2} \right )$ makes sense when $\alpha \neq \pi + 2k\pi, k \in \mathbb{Z}$: henceforth, we will assume that this condition is met.

By definition of tangent function, we have: $$\tan \left ( \frac{\alpha}{2} \right ) = \frac{ \sin \left ( \frac{\alpha}{2} \right )}{\cos \left ( \frac{\alpha}{2} \right )}$$

When $\alpha \neq 2k \pi, k \in \mathbb{Z}$, we can multiply numerator and denominator by $\sin \left ( \frac{\alpha}{2} \right )$, because this quantity is non-zero. We therefore get:

$$\tan \left ( \frac{\alpha}{2} \right ) = \frac{ \sin^2 \left ( \frac{\alpha}{2} \right )}{\cos \left ( \frac{\alpha}{2} \right ) \cdot \sin \left ( \frac{\alpha}{2} \right )}. $$

For what we saw earlier: $$\sin^2 \left ( \frac{\alpha}{2} \right ) = \frac{1 - \cos \alpha}{2}$$and instead, applying the sine duplication formula: $$\cos \left ( \frac{\alpha}{2} \right ) \cdot \sin \left ( \frac{\alpha}{2} \right ) = \frac{1}{2} \sin \alpha$$

In conclusion we get the following formula: $$\tan \left ( \frac{\alpha}{2} \right ) = \frac{ 1 - \cos \alpha}{\sin \alpha}.$$

If in the expression of the tangent we had multiplied numerator and denominator by $\cos \left ( \frac{\alpha}{2} \right )$ then with steps similar to what we have done we get another formula:$$\bbox[5px,border:2px solid #118D45]{\tan \left ( \frac{\alpha}{2} \right ) = \frac{\sin \alpha}{1 + \cos \alpha}}. \tag 2 $$

We note that it always holds $\cos \left ( \frac{\alpha}{2} \right ) \neq 0$ since we have imposed $\alpha \neq \pi + 2k\pi, k \in \mathbb{Z}$ (and this entitles us to multiply numerator and denominator by this term).

Is there a faster and more immediate proof of the $(1)$ or $(2)$?

vitamin d
  • 5,913
Sebastiano
  • 8,290
  • 2
    Your proof looks me nice . Maybe no need another one :) – lone student Feb 26 '21 at 23:59
  • 1
    @lonestudent Thank you very much for your compliment. But it is for my students. Unfortunately, they want everything and immediately. As soon as I do a few more steps they find serious difficulties. – Sebastiano Feb 27 '21 at 00:02
  • 1
    I back up the comment by lonestudent, the proof is neat as it is (and also very understandable). – Severin Schraven Feb 27 '21 at 00:11
  • 1
    I think there is a small technicality: you only assumed in your proof that $\alpha \neq \pi + 2\pi k$, but you used that $\alpha \neq 2 \pi k$. It would be better to remark at the start of the proof that the LHS only makes sense when $\alpha \neq \pi + 2\pi k$ (as you did) and that the RHS only makes sense when $\alpha \neq \pi k$ (and therefore we should assume that $\alpha \neq \pi k$ for this proof). – diracdeltafunk Feb 27 '21 at 00:14
  • @SeverinSchraven I agree with you but I am so happy in my teacher role that I am adapting to students who want the two-step proofs. – Sebastiano Feb 27 '21 at 00:14
  • @diracdeltafunk Hi, I remember that now I'm sleeping and I am very tired. You can post an answer with your comment. I like vote up the used. Good night. – Sebastiano Feb 27 '21 at 00:16
  • 2
    @Sebastiano: This question offers a diagrammatic proof. My answer refines it a little. – Blue Feb 27 '21 at 00:32
  • @Blue Last night my eyes was closed :-(...I hope that you and another user close my question. With a lot of sincerity for my humble opinion it is a duplicate. I am very happy to have voted up all the users. My sincere best regards. – Sebastiano Feb 27 '21 at 13:11
  • 1
    @Sebastiano: I've closed the question. Finding previous incarnations of a question isn't always easy (searchings for equations is tricky), so don't feel bad. :) ... BTW: You mention in a comment that you're seeking an alternative approach on behalf of your students. (Good for you!) Whenever you do this, please include that motivation as part of the question, as it's useful context that should in turn motivate answerers. Cheers! – Blue Feb 27 '21 at 13:30
  • 1
    @Blue Thank you very much to have closed the question that is a duplicate. I have put only the tag education (like an implicit suggestion for students of an high school). I will remember of your precious comment. Grazieeeeeeeeee. – Sebastiano Feb 27 '21 at 20:31

4 Answers4

3

Here are geometric proofs, which I believe are "faster and more immediate", as the OP desired.

All you need is the "circle theorem" that "the angle at the circumference is half the angle at the center".

First, the (somewhat easier) proof for $$\tan\left(\frac{\alpha}{2}\right)=\frac{\sin{\alpha}}{1+\cos\alpha}$$

proof1

Second, the one OP requested, that $$\tan\left(\frac{\alpha}{2}\right)=\frac{1-\cos\alpha}{\sin\alpha}$$

proof2

I recognise that the picture works only for acute $\alpha$, but it is easy to see how it can work for obtuse or reflex $\alpha$.

Benjamin Wang
  • 4,667
2

We could multiply both sides by $\sinα$

Then on the LHS use the double angle for $\sinα = 2\sin(α/2) \cos(α/2)$ and put $\tan(α/2)=\sin(α/2)/\cos(α/2)$ then the LHS becomes $2\sin^2(α/2)$.

The RHS is the same as $1-\cosα = 1-(1-2\sin^2(α/2))$ from a double angle formula for $\cosα$, so it's true.

Sebastiano
  • 8,290
John Hunter
  • 691
  • 4
  • 13
2

Replace $\alpha$ by $2\beta$ so that the right side is $${{1-\cos 2\beta}\over {\sin 2\beta}}= {{1-(\cos^2\beta-\sin^2\beta)}\over {2\sin\beta\,\cos\beta}}$$

$$={{2\sin^2\beta}\over{2\sin\beta\cos\beta}}= {{\sin\beta}\over {\cos\beta}}=\tan\beta$$

David
  • 21
1

By request, I am writing my comment as an answer:

I think there is a small technicality: you only assumed in your proof that $α≠π+2πk$, but you used that $α≠2πk$. It would be better to remark at the start of the proof that the LHS only makes sense when $α≠π+2πk$ (as you did) and that the RHS only makes sense when $\alpha≠πk$ (and therefore we should assume that $α≠πk$ for this proof).

diracdeltafunk
  • 16,589