4

I am trying to find the smallest number of "crosses" needed to cover an n by n square with overlap.
A "cross" is basically the "X" pentomino, the following figure:

figure 1

The problem is to place the smallest number of crosses so that each cell is covered at least once.
The crosses are placed by picking the point for their center. They may overlap with each other and
they do not have to fit entirely on the board - for example, you can place a cross at the cell $(0,0)$.
Which would produce the following:

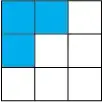
figure 2

I would like to know whether there exists a polynomial-time algorithm for finding an optimal solution (finding the positions of the crosses). Clearly there are some patterns that achieve a good covering, but I would like to have a proof or decent argument why such a covering is the best possible.
I have checked $n = 1,2,3,4,5,6,7$. The minimal number of crosses are: $1,2,3,4,7,10,12$
Here are some examples of how such coverings might be achieved (green cells are the centers of the crosses):
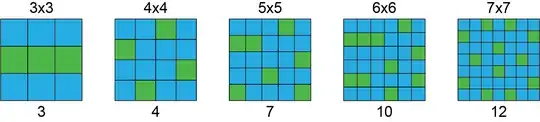
figure 3

evolved_antenna
  • 71
  • 2
    The knight move seems to be involved in these coverings. Maybe tilling the plane like this http://www.projet-ermitage.org/ARMT/images/22rmti_fr-8a.png and just take the bounding square ? This gives an upper bound anyway. Lower bound seems more difficult to find. – zwim Feb 20 '21 at 22:54
  • 3
    See https://oeis.org/A104519 for earlier work. – Gerry Myerson Feb 20 '21 at 23:04
  • 1
    See this recent question for an extremely similar problem, though with a more modest goal. Do these two questions originate from the same source, or is this one inspired by that one? – RavenclawPrefect Feb 20 '21 at 23:07
  • I found out that every time you cover one corner there's at least two unit squares "wasted", i.e. overlapped or out of the $n\times n$ square. So the smallest number $m_n>(n^2+8)/5$, at least for $n>6$. – atzlt Feb 21 '21 at 03:25
  • 1
    I’m voting to close this question because it seems to be based on a problem from a running competition: Mathcamp 2021, deadline March 18. – Jaap Scherphuis Feb 24 '21 at 10:21
  • @JaapScherphuis The question is not related to the mentioned contest. I got the idea while I was playing a game - Stardew Valley. In the game you can use sprinklers to water your crops, the basic ones water the 4 blocks around them. So I was curious as to what the smallest number of sprinklers necessary was. The said sprinkler. – evolved_antenna Feb 25 '21 at 08:03

0 Answers0