If a two variable smooth function has two global minima, will it necessarily have a third critical point?

Question

Assume that $f:\mathbb{R}^2\to\mathbb{R}$ a $C^{\infty}$ function that has exactly two minimum global points. Is it true that $f$ has always another critical point?

---

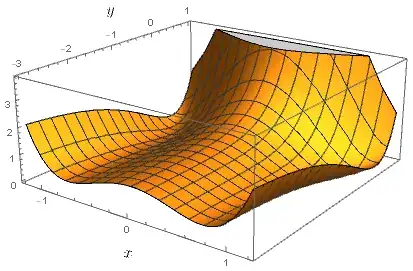
A standard visualization trick is to imagine a terrain of height $f(x,y)$ at the point $(x,y)$, and then imagine an endless rain pouring with water level rising steadily on the entire plane.

• Because there are only two global minima, they must both be isolated local minima also. Therefore, initially the water will collect into two small lakes around the minima.
• Those two points are connected by a compact line segment $K$. As a continuous function, $f$ attains a maximum value $M$ on the set $K$. This means that when the water level has reached $M$, the two lakes will have been merged.
• The set $S$ of water levels $z$ such that two lakes are connected is thus non-empty and bounded from below. Therefore it has an infimum $m$.
• It is natural to think that at water height $m$ there should be a critical point. A saddle point is easy to visualize. For example the function (originally suggested in a deleted answer) $f(x,y)=x^2+y^2(1-y)^2$ has a saddle point at the midway point between the two local minima at $(0,0)$ and $(0,1)$. But, can we prove that one always exists?

---

Follow-ups:

• Does the answer change, if we replace $\Bbb{R}^2$ with a compact domain? What if $f$ is a $C^\infty$ function on a torus ($S^1\times S^1$) or the surface of a sphere ($S^2$). Ok, on a compact domain the function will have a maximum, but if we assume only isolated critical points, what else is implied by the presence of two global minima?
• Similarly, what if we have local minima instead of global?
• If it makes a difference you are also welcome to introduce an extra condition (like when the domain is not compact you could still assume the derivatives to be bounded - not sure that would be at all relevant, but who knows).

Answer 1

With respect to the first part of your question: No, a function with two global minima does not necessarily have an additional critical point. A counterexample is $$ f(x, y) = (x^2-1)^2 + (e^y - x^2)^2 \, . $$ $f$ is non-negative, with global minima at $(1, 0)$ and $(-1, 0)$.

If the gradient $$ \nabla f(x, y) = \bigl( 4x(x^2-1) - 4x(e^y - x^2) \, , \, 2e^y(e^y-x^2) \bigr) $$ is zero then $e^y =x^2$ and $x(x^2-1) = 0$. $x= 0 $ is not possible, so that the gradient is zero only if $x=\pm1$ and $y=0$, that is only at the global minima.

The construction is inspired by Does $f$ have a critical point if $f(x, y) \to +\infty$ on all horizontal lines and $f(x, y) \to -\infty$ on all vertical lines?. We have $f(x, y) = g(\phi(x, y))$ where:

• $g(u, v) = (u^2-1)^2 + v^2$ has two global minima, but also an additional critical point at $(0, 0)$, and
• $ \phi(x, y) = ( x , e^y-x^2)$ is a diffeomorphism from the plane onto the set $\{ (u, v) \mid v > -u^2 \}$. The image is chosen such that it contains the minima of the function $g$, but not its critical point.

With respect to the “connected lakes” approach: The level sets $$ L(z) = \{ (x, y) \mid f(x, y) \le z \} $$ connect the minima $(-1, 0)$ and $(1, 0)$ exactly if $z > 1$. The infimum of such levels is therefore $m=1$, but $L(1)$ does not connect the minima (it does not contain the y-axis). Therefore this approach does not lead to a candidate for a critical point.

---

The above approach can also be used to construct a counterexample with bounded derivatives. Set $f(x, y) = g(\phi(x, y))$ with

• $g(u, v) = \frac{(u^2-1)^2}{1+u^4} + \frac{v^2}{1+v^2}$, which has two global minima at $(\pm 1, 0)$, one critical point at $(0, 0)$, and bounded derivatives.
• $\phi(x, y) = (x, \log(1+e^y) +1 -\sqrt{1+x^2} )$, which is a diffeomorphism from $\Bbb R^2$ with bounded derivatives onto the set $\{ (u, v) \mid v > 1- \sqrt{1+v^2} \}$, which contains the points $(\pm 1, 0)$ but not the point $(0, 0)$.

Answer 2

$ \def\norm#1{\lVert#1\rVert} $The answer to the question as stated is no as Martin showed, but is yes if we add the condition that $f(x)→∞$ as $\norm{x}→∞$. Martin's example pushes the saddle point 'to infinity', which would be blocked by this condition. And we do not need global minima, nor even continuous derivatives!

Theorem. Take any differentiable $f : ℝ^2→ℝ$ such that $f$ has at least two local minima and $f(x)→∞$ as $\norm{x}→∞$. Then $f$ has a third stationary point.

Proof. Let $a,b$ be two (distinct) local minima of $f$. Let $L$ be the straight line segment from $a$ to $b$, and let $m$ be the maximum value of $f$ on $L$ by EVT (extreme value theorem). For each $k∈ℕ$ let $T(k)$ be a regular tiling of $ℝ^2$ by (closed) hexagons each with diameter $2^{-k}$ such that $a,b$ are respectively in the interior of some hexagonal tile $A,B$. Define the height of each tile $H$ in $T(k)$ to be the minimum value of $f$ on $H$, which exists by EVT. Note that if any tile $H$ has height no greater than that of all its neighbouring tiles, then $f$ has a local minimum on $H$, so we can assume that every tile besides $A$ or $B$ has height greater than that of some neighbour. Impose an enumeration on the tiles in $T(k)$ (say in hexagonal rings outward from $A$). For any tiles $G,H$, we say that $G$ is higher than $H$ (and that $H$ is lower than $G$) iff either ( $G$ has height higher than $H$ ) or ( $G,H$ have the same height but $G$ is after $H$ in the enumeration ). Note that for each tile $H$ there are only finitely many tiles lower than $H$ (since $f(x)→∞$ as $\norm{x}→∞$).

Then from any tile $H$ we can reach $A$ or $B$ via a downhill path, defined as a connected sequence of tiles each of which is higher than the next, because iteratively moving to a lower tile must terminate eventually. Thus there is a good tile, defined to be a tile of height at most $m$ from which we can reach both $A$ and $B$ each via a downhill path, because $L$ passes through a finite connected sequence of tiles from $A$ to $B$, and that sequence has consecutive tiles $I,J$ such that there is a downhill path from $I$ to $A$ and a downhill path from $J$ to $B$, so either $I$ or $J$ is a good tile. Let $M(k)$ be the lowest good tile, and let $O(k)$ be the centre of $M(k)$. Note that the second tiles of any downhill paths $P,Q$ from $M(k)$ cannot be adjacent, otherwise the higher one of those tiles would be a good tile lower than $M(k)$.

Observe that $O$ is a bounded sequence because each term is within distance $1$ from some point in $\{ x : x∈ℝ^2 ∧ f(x) ≤ m \}$, and the latter is bounded. Thus by BZ (Bolzano-Weierstrass) there is some strictly increasing sequence $i : ℕ→ℕ$ and point $c∈ℝ^2$ such that $\lim_{k→∞} O(i(k)) = c$.

From now let us assume that $f$ has only two local minima. By the local minimum of $f$ at $a$, there is some closed annulus $D$ around $a$ with inner radius $r$ and outer radius $s$ with $0<r<s<|L|$ such that $f{↾}D ≥ f(a)$. Let $u = \min_{x∈D} f(x)$. Then $u > f(a)$, otherwise $f$ has a local minimum in $D$ different from $a$ and $b$. And for all sufficiently large $k$ every downhill path from a good tile in $T(k)$ must pass through some tile contained within $D$, and so $M(k)$ has height at least $u$. Symmetrically, there is some $v > f(b)$ such that $M(k)$ has height at least $v$ for all sufficiently large $k$. Since $i$ is strictly increasing, we thus have $f(c) = \lim_{k→∞} f(O(i(k))) ≥ \max(u,v)$ and hence $c∉\{a,b\}$.

If $f$ is stationary at $c$, then we are done. Otherwise, there is some nonzero linear $g : ℝ^2→ℝ$ such that $f(c+t) ∈ f(c)+g(t)+o(\norm{t})$ as $t→⟨0,0⟩$, and hence for some sufficiently large $k$ we have that $M(k)$ and its neighbours are sufficiently close to $c$ that those neighbours lower than $M(k)$ are consecutive around $M(k)$ and number at most four. ^[1]

Let $P$ be a downhill path from $M(k)$ to $A$ and $Q$ be a downhill path from $M(k)$ to $B$, and let $R,S$ be the second tiles of $P,Q$ respectively. We now have two cases (up to symmetry):

(Case 1)
There is only one neighbour $X$ of $M(k)$ between $R$ and $S$:
$X$ must be lower than $M(k)$. If $X$ is higher than $R$ or $S$, then the combined path $P{+}Q$ can be altered to pass through $X$ instead of $M(k)$, so one of $X,R,S$ would be a good tile. If $X$ is lower than both $R$ and $S$, then since $X$ has a downhill path to $A$ or $B$, respectively $S$ or $R$ would be a good tile.

(Case 2)
There are two lower neighbours $X,Y$ of $M(k)$ between $R$ and $S$:
If $X$ is higher than $R$ or $Y$ is higher than $S$, then we can insert $X$ or $Y$ respectively into $P{+}Q$, which yields an instance of Case 1. If $X$ is lower than $R$ and $Y$ is lower than $S$, then by symmetry we can assume that $X$ is lower than $Y$, and so since $X$ has a downhill path to $A$ or $B$, respectively $S$ or $R$ would be a good tile.

In both cases, this contradicts minimality of $M(k)$. Therefore $c$ is indeed the point we are looking for.

−−−−−−−

^[1] This part is kind of painful to prove rigorously, but it should be clear from a diagram.

Answer 3

In 2019, I posted an answer to a relevant question. See: Can a multivariate function only have local minimum?, and Can a smooth function with compact sublevel sets only admit local minimizers?

In [1], some examples are given.

The function $f(x, y) = (x^2-1)^2 + (x^2y-x-1)^2$ has exactly two stationary points $(-1, 0), \ (1, 2)$ which are both strictly local minima (also are both global minima). There is no another stationary point.

The function $f(x,y) = -\mathrm{e}^{-x} (x\mathrm{e}^{-x} + \cos y)$ has infinitely many strictly local minima. There is no another stationary point.

Reference

[1] Alan Durfee, Nathan Kronefeld, Heidi Munson, Jeff Roy and Ina Westby, “Counting Critical Points of Real Polynomials in Two Variables,”, The American Mathematical Monthly, Vol. 100, No. 3 (Mar., 1993), pp. 255-271.

Answer 4

Morse theory says that every Morse function $f$ (that is all critical points were non-degenerate and distinct critical points take distinct critical values) satisfies $$\#\min+\#\max-\#\mathrm{saddle}=\chi(M).$$ So, in the case of torus (that its Euler char is $0$), the functions must have $\#\mathrm{saddle}=\#\max+2$. By the fact that all continuous functions on a compact domain attaint at least a max and a min therefore we should have at least a max point then at least 3 saddle point for torus. in the case of sphere is similar. $\#\min+\#\max-\#\mathrm{saddle}=\chi(\Bbb S^2)=2$ so having two global minima we must have $\#\max=\#\mathrm{saddle}\neq 0$. In any case we have at least a saddle point.

Note that these are non-degenerate critical points (that means Hessian is nonsingular at that points) and there is a function on torus with 3 critical points i.e. a min, a max and a degenerated saddle point.

Answer 5

Suppose we have a compact orientable manifold $M$ with boundary $\partial M$. Suppose that we have a Morse function $f$ whose gradient flow is transverse to the boundary $\partial M$. Then the boundary splits into two components (which are themselves not necessarily connected) $\partial M=\partial_- M^{}+\partial_+M$ where $-\nabla f$ points outward on $\partial_-M$ and inward along $\partial_+M$. Then we have relative Morse inequalities. Define $b_k=\mathrm{rank} H_k(M,\partial M)$ and $c_k$ the number of critical points of $f$ of index $k$. Define the relative Poincare Polynomial and Morse polynomial $$ P_t(M,\partial_- M)=\sum_{k=0}^n b_k \qquad M_t(f)=\sum_{k=0}^n c_k. $$ The Morse relations state that there exists a polynomial $Q_t$ with non-negative coefficients $Q_t$ such that $$ M_t(f)=P_t(M,\partial_- M)+(1+t)Q_t $$ An immediate consequence is that the number of critical points of index $k$ must be larger than the $k$-th Betti number of $(M,\partial_-M)$. And that the alternating sum of the number of critical points of index $k$ must equal the relative euler characteristic of $(M,\partial_-M)$ (evauate the expression above at $t=-1$). In general the Morse relations are stronger than the corollaries I just outlined.

For non-compact manifolds the relation is a bit more complicated, and growth conditions on $f$ should be given. (But the statement for compact manifolds with boundary should give you an idea what to expect). But there are weaker conditions available than demanding that $\lim_{|x|\rightarrow \infty}f(x)=\infty$ (A keyword is isolation or Palais-Smale). You can also make sense of this for non-Morse functions, or even more general vector fields (beyond the gradient of function). This is known as Conley theory. You can have a look at my phd thesis where I discuss some of these matters.

Answer 6

We want to explain the intuition in the OP : at the level where the lakes join, there exists a critical point.

Let $M$ be a topological space that is normal, locally path connected and path-connected (like a connected manifold).

Let $f$ be a continuous proper map $f\colon M \to \mathbb{R}$. Moreover, let $b$ a point of local minimum of $f$, and $a\ne b$ such that $f(a) \le f(b)$. Then there exists $c\ne a,b$ that is critial point of $f$.

Definition 1.: $c\in M$ is a critical point of $f$ if $c$ is a local minimum of $f$, or for every $D$ neighborhood of $c$ the set $D \cap M_{< f(c)}$ is not connected (think of a saddle point).

Definition 2. The points $a$, $b$ of a topological space $X$ are separated in $X$ if there exists a partition of $X$ into open (close) subsets $U$, $V$, with $a \in U$, $b\in V$.

On to the proof. First, some easy things: consider $U$ an open subset $b$ not containing $a$, such that $f(b) \le f(x)$ for all $x \in U$. Let $b \in V$ open such that $\overline V \subset U$. If for some point $y \in \partial V$ we have $f(y) = f(b)$, then $y$ is again a local minimum. Let's not allow this possibility. Therefore, we have $f(x) > f(b)$, for all $x \in \partial V$. Note that $a \in M \backslash \overline V$, and $b \in V$. Therefore, we get $a$, $b$ separated in $M_{\le f(b)}$.

Now let us show : if $a$, $b$ are separated in $M_{\le t}$, then there exists $\delta> 0$ such that $a$, $b$ separated in $M_{\le t+\delta}$. Indeed, let $C\ni a$, $D\ni b$ closed, disjoint, with union $M_{\le t}$. Consider $U$, $V$ disjoint open subsets, $C\subset U$, $D\subset V$. Note that $f^{-1}(t) \subset U \cup V$. Since $f$ is proper, there exists $\delta> 0$ such that $f^{-1}([t, t+\delta]\subset U\cup V$. We conclude that $M_{\le t+\delta} \subset U\cup V$. We get a separation of $a$, $b$ in $M_{\le t+\delta}$.

Since $M$ is path-connected, there exists $\gamma$ a path from $a$ to $b$. Let $s= \sup_{\gamma} f$. We conclude that $a$, $b$ are in the same component of $M_{\le s}$, so they are not separated in $M_{\le s}$.

Consider the set $$\{ t \in [f(b), \infty) \ | \ a, b \textrm{ separated in } M_{\le t} \}$$

Since the $s$ above in not in the set, we conclude that the set is bounded, so it has a supremum $t^*$. Now, $t^*$ is not in the set, by the above.

Now, we have $a$, $b$ in the open subset $M_{< t^*}$. Can $a$, $b$ in the same component? If they were, we would have ( locally path-connectedness!) a path $\eta$ from $a$ to $b$ in $M_{< t^*}$. But that would mean that $a$, $b$ are not separated in some $M_{\le t^*-\epsilon}$, contradiction.

Therefore, we have $U$, $V$ disjoint open subsets, $a\in U$, $b\in V$, $U\cup V = M_{< t^*}$.

Now, consider $\overline M_{< t^*} \subset M_{\le t^*}$. If the inclusion were strict, we would have $c \in M_{= t^*}$ that is a local minimum, done.

Let's assume now that $\overline M_{< t^*} = M_{\le t^*}$, and so $\overline U \cup \overline V = M_{\le t^*}$. The sets $\overline U$, $\overline V$ cannot be disjoint, since then we woud have a separation of $a$, $b$ in $M_{\le t^*}$. Let then $c \in \overline U \cap \overline V$. We have $f(c) = t^{*}$, and for every $D$ neighborhood of $c$, we have $D\cap M_{< f(c)} = (D\cap U) \cup (D\cap V)$. Hence, $D\cap M_{< f(c)}$ is not connected. We conclude that $c$ is a critical point.

$\bf{Note:}$ In the example of @Martin R: $f(x,y) = (x^2-1)^2 + (e^y-x^2)^2$, the level set $f^{-1}(t)$ looks like OO for $t \in (0, \frac{1}{2})$, like $\cap \cap$ for $t\in [\frac{1}{2},1]$ and like M for $t > 1$. Worth understanding.