1

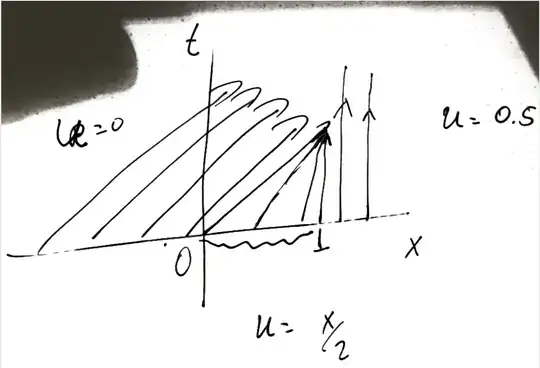
My teacher just went over the method of characteristics and we did an example with shocks then drew a picture, but I wanted to clarify some things for myself.

The example was $$u_t + (1-2u) u_x = 0$$ such that $u(x,0 )= \begin{cases} 0 & x\leq 0 \\ 0.5 & \geq 1 \\ x/2 & \text{otherwise} \end{cases} $

So from my understanding due to the method of characteristics I get two ODEs $\frac{dx}{dt}= 1-2u$ and $\frac{du}{dt} = 0$ where $u = u(x(t),t)$. Solving the second equation first I get $u(x(t),t) = u_0$. Now depending at $x(t)$ I have three different options $0,0.5$, and $x/2$.

Where I am confused is he drew the picture, I am attaching. I get the characteristics for $x<0$ and $x>1$. However, I do not understand how he obtained the characteristics in the middle region. That ODE should be $\frac{dx}{dt} = 1-x$ Which I can use sep of variables to get $\frac{1}{1-x}dx = 1dt$ and from there , I get $-ln|1-x| = t + x_0$ so from my understanding the characteristics should look like logarithms. I would greatly appreciate some clarification on this, thank you.

enter image description here

Calvin Khor
  • 36,192
  • 6
  • 47
  • 102
Kori
  • 1,530

1 Answers1

3

The initial derivation is correct. From $\frac{du}{dt} = 0$ we deduce that $u(t)=u_0$ is constant along the characteristic curves, and from $\frac{dx}{dt} = 1-2u$ we deduce that these curves are straight lines with equation $x(t) = (1-2u_0) t + x_0$ where $x(0) = x_0$. Their slope $1-2u_0$ is deduced from the initial value $u(x_0,0) = u_0$ at the abscissa $x_0$, i.e. \begin{equation} x(t) = \left\lbrace\begin{aligned} & t + x_0, & & x_0 \leq 0\\ & x_0, & & x_0 \geq 1\\ & (1-x_0) t + x_0 , & &\text{otherwise} \end{aligned}\right. \end{equation} In the $x$-$t$ plane, the first family consists of lines parallel to the identity function, the second family produces vertical lines, and the last one produces lines with variable slope. The formation of shocks is described in this post and related ones.

EditPiAf
  • 21,328