Rotation number of non-invertible continuous map of $S^1$

Question

Recently I have been studying rotation numbers and all sources I came across define them for invertible circle maps $A$. But what breaks, when $A$ is not bijective? I.e...

Let $A: \mathbb{R} \to \mathbb{R}$ be a continuous map such that $A(y + 1) = A(y) + 1$. For $y \in \mathbb{R}$ let its rotation number be given by $$ \rho_y(A) := \lim\limits_{k \to \infty} \frac{A^k(y) - y}{k}. $$

Suppose now $A$ is non-invertible.

• Then can $\rho_y$ exist?
• If so, is $\rho_y$ independent of $y$?

I would be very grateful about a hint or two where to start.

---

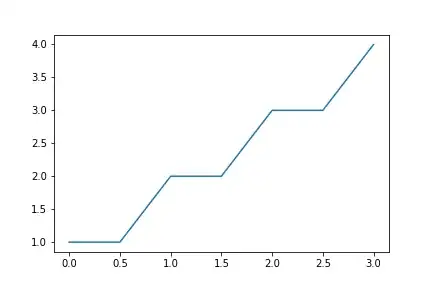
So I came up with the following example: For $s \in \mathbb{R}$ let $$ A(y) = \begin{cases} \lfloor y \rfloor + s &\text{ if } & y \mod 1 \leq \frac{1}{2} \\ 2y - \lfloor y \rfloor - 1 + s &\text{ else } & \end{cases}. $$ $A$ fulfills the requirements stated above and is not injective.

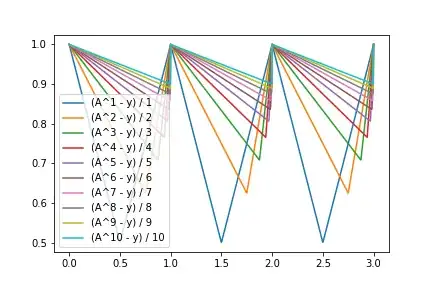
And empirically we have $\rho_y(A) = s$:

So $\rho$ does exists and is independent of $y$.

Proof (Idea):

Bound $A(y)$ from below by $L(y) = \lfloor y \rfloor + s$ and from above by $U(y) = y + s.$ Then sandwich $\rho_y(A)$.

Answer 1

Here's a counterexample to $\rho_y$ being constant.

Suppose $A(0)=0, A(0.5) = 1.5, A(1)=1$, e.g. use linear interpolation, and extend this by periodicity. Note that $A$ cannot be bijective by the intermediate value theorem.

Clearly $\rho_0 = 0$. However, $A(0.5) = 1.5$, $A(1.5) = A(0.5) + 1 = 2.5$, and in general $A^n(0.5) = n + 0.5$. Thus $\frac{A^n(0.5) - 0.5}{n} = 1$, so $\rho_{0.5} = 1 \neq 0 = \rho_0$.

Edit: I think I have a counterexample in principle for existence of $\rho_y$ as well, but writing out the details precisely would be very messy.

The idea is to have two locations, $0$, and $y^*$, where for $y$ near $0$, $A(y) \approx y$, but for $y$ near $y^*$, $A(y^*) \approx y^* + 1$. Now you want to arrange it so that there is some orbit which alternates periods of time near 0 and $y^*$ in such a way that it spends exponentially more time near each limit point after each visit. In that case, the limit won't exist for roughly these reasons.

How do we get the orbit to behave this way? Well, if we consider $A(y) = 0.5 y$, then for $y>0$ small we'll get "attraction" towards $0$, and if we consider $A(y) = 2y$, then for $y<0$ small we'll get "repulsion" away from $0$. So, start with the $A(y) = 0.5 y$ behavior headed towards $0$, but then after some number of iterations make $A(y)$ slightly negative, letting the $A(y) = 2y$ repulsion kick in until we're far enough from $0$ that we can just head to $y^* + \epsilon$. Make a similar attractor/repulser setup near $y^*$. When you head back to $0+\epsilon'$, make sure you pick $\epsilon'$ small enough that it's "closer in" than the point where you made $A(y)$ slightly negative the first time, and then repeat the whole thing infinitely many times.

You do need to make sure the "slightly negative" values you pick will, after the repulsion step, get you to exactly where you want to be near the other limit point. That's possible using an $A(y) = 2y$ repulser directly since its iterates are simply $A^n(y) = 2^n y$ and you can reverse-engineer the initial $y$ easily from its target value.