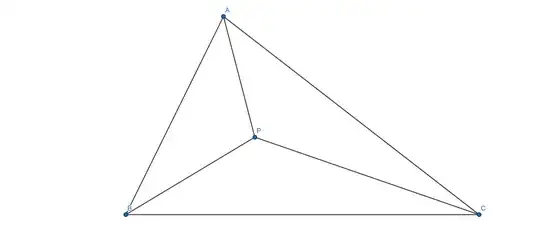
Find the locus of all points inside $\triangle ABC$ such that $PA^{2}+PB^{2}=PC^{2}$.
At first, i tried finding a right angled triangle and then tried to go on applying Pythagorean Theorem and finding other trivia but that didn't seem to work. I think the locus is most likely to be some line segment rather than an arc of some circle as that seems to be quite unrelated seen from an Euclidean perspective. Applying Apollonius' Theorem and Stewart's Theorem on some triangles might be the key to this problem although i could not find such triangles. I don't know whether this can be solved by trigonometry or not but since this is a problem from a chapter on euclidean geometry, i am sure that there is some clever way to look at this problem.