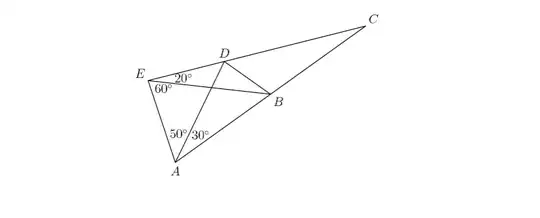
In the triangle shown, what is the degree measure of $\angle ADB$
I have mainly tried angle-chasing, but it turns out that through plain angle-chasing you cannot find $\angle ADB$ or $\angle EBD$. I explored extending $AE$ and $BD$ to their intersection, but that did not help much either. Can someone get me started on how to solve this problem? I have a feeling dropping a line from $B$ to $DC$ might help, but I cannot figure out which line it would be. EDIT: I realized that dropping a line from B to DC which is parallel to EA might work.
Thanks,
Mike