10

I have noticed that the following simple sum of Laguerre polynomials (weighted with alternating signs) seems to be positive for any $N$ when $x>0$:

$$\sum_{k=0}^{N}\;(-1)^{k}\;L_{k}(x)$$

More precisely, when $N$ is even, the sum is positive $\forall\;x$ and when $N$ is uneven, the sum has only one zero in $x=0$.

I have checked this numerically up to $N=10{}^{2}$.

I cannot find any reference to this sum in the literature. Are my observations correct? If this is a known result, could someone point me in the right direction to find a reference or some documentation for this?

metamorphy
  • 43,591
Lucky
  • 133
  • Is it linked with quantum mechanics? – LL 3.14 Feb 04 '21 at 12:29
  • Yes, it is related to a research work I am doing in relation to the Wigner phase space. My assertion above implies that a mixture with equal probabilities of the N first Fock states has a positive Wigner function (regardless of N). Actually, I thought this was a known result (so I expected more a reference to some literature/article than calculations). – Lucky Feb 04 '21 at 18:48
  • Ahah, as I expected. I arrived on this page exactly by looking on this same mixture with equal probability. But I am trying to prove that it converges to the an indicator function in the limit $N = \hbar^{-1} \to \infty$ – LL 3.14 Feb 04 '21 at 20:13

3 Answers3

2

Here is an additional remark.

Let us denote by $$ g_N(x) := \sum_{n=0}^N (-1)^n L_n(x) $$

1) When $x≤0$. First, since $L_n(x) = \sum_{k=0}^n \binom{n}{k} \frac{(-x)^k}{k!}$, we immediately have for $x≤0$ $$ g_N(x) = \sum_{n=0}^N \sum_{k=0}^n \binom{n}{k} \frac{|x|^k}{k!} ≥ 0 $$

2) When $x≥0$.

  • When $m = 2N+1$ is odd, by the answer of @mathreadler, one has $$ g_{2N+1}(x) = \sum_{n=0}^N L_{2n}(x)-L_{2n+1}(x) = \int_0^x \sum_{n=0}^{N} L_{2n}(x)\,\mathrm d x $$ Now, recall the formula $\sum_{n=0}^{m} L_{n} = L_m^{(1)} = -L'_{n+1}$ (see e.g. wikipedia). Thus since $\frac{1+(-1)^n}{2} = \mathbf{1}_\text{n even}$, $$ 2\,g_m(x) = \int_0^x \sum_{n=0}^{m} (1+(-1)^n)\, L_{n}(x)\,\mathrm d x = \int_0^x g_{m}(x) + L^{(1)}_{m}(x)\,\mathrm d x $$ and so since $L_{2N+2}(0)=1$, for $m=2N+1$ any odd positive number, one has $$ 2\,g_{m}(x) = \int_0^x g_{m}(t) \,\mathrm d t - L_{m+1}(x) + 1 $$ Taking the derivative, it tells that $$ g_m' = \frac{1}{2} \,g_m + \frac{1}{2} L^{(1)}_{m}. $$ Since $g_m(0)=0$, we can then solve this differential equation to get $$ 2\,e^{-x/2}\,g_m(x) = \int_0^x L^{(1)}_{m}(t) \,e^{-t/2}\,\mathrm d t $$

$\bullet$ Similarly, when $n=2N$ is even, removing the first term $L_0(x) =1$ of the sum, $$ g_{2N}(x) = 1- \sum_{k=1}^N L_{2k-1}(x)-L_{2k}(x) = 1-\int_0^x \sum_{k=1}^{N} L_{2k-1}(x)\,\mathrm d x \\ = 1-\int_0^x \sum_{k=0}^{2N} \frac{1-(-1)^k}{2}\,L_{k}(x)\,\mathrm d x $$ so $$ g_n(x) = 1 + \frac{1}{2}\int_0^x (g_n - L_{n}^{(1)}) $$ and so $$ g_n' = \frac{1}{2} (g_n - L_{n}^{(1)}) $$ and so since $g_n(0)=1$, $$ 2\,e^{-x/2}\,g_n(x) = 2 - \int_0^x L^{(1)}_{n}(t) \,e^{-t/2}\,\mathrm d t $$ which is positive if $\int_0^x L^{(1)}_{n}(t) \,e^{-t/2}\,\mathrm d t < 2$.

3) Conjecture.

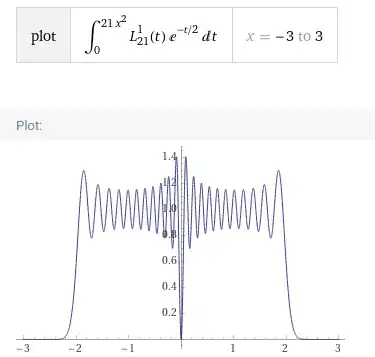
When $N\to\infty$, $2\,e^{-N|x|^2/2}\,g_N(N|x|^2)$ approaches $\mathbb 1_{[-2,2]}$. Graph

LL 3.14
  • 13,938
  • Thank you very much for this detailed answer (actually, I expected more a reference to an existing result than a new calculation). I have only browsed through the calculations and before digging into them, I had a question about the last step: we expect the integrand to be positive for t>=0 but the limits of the last integral run from -x to 0 with x positive. Shouldn't we focus on the value of the integrand for t<=0 ? – Lucky Feb 04 '21 at 18:39
  • Oh yes, you are right, it is not working right now ... except when $x≤0$ ... there must be a more precise estimate? I keep the post as an additional remark ... – LL 3.14 Feb 04 '21 at 20:17
  • Can it help addressing your conjecture to notice (by using the generating function for Laguerre polynomials) that $\sum_{n=0}^{\infty}u^{n}\left(-1\right)^{n}L_{n}\left(x\right)=e^{ux/\left(1+u\right)}/(1+u)$ , which implies that $g{}_{N}\left(x\right)\rightarrow e^{x}:\forall x$ when $N\rightarrow\infty$. – Lucky Mar 07 '21 at 13:15
  • I should have written $g{}_{N}\left(x\right)\rightarrow e^{x/2}/2:\forall x>0$ when $N\rightarrow\infty$ – Lucky Mar 07 '21 at 16:33
2

It is proved in https://arxiv.org/abs/2104.14996 that the Wigner function of the equally weighted mixture of the first $M+1$ Fock states is nonnegative, for all $M>=0$.

This proves that the sum in my question is indeed nonnegative because the Wigner function of this equally weighted mixture has the form (in polar coordinates): $\frac{1}{\left(M+1\right)}\sum_{n=0}^{M}\frac{\left(-1\right)^{n}}{\pi}\:L_{n}\left(2r^{2}\right)\:e^{-r^{2}}$.

Lucky
  • 133
1

Maybe some help on the way but not a full answer.

According to Wikipedia, Laguerre polynomials build a Sheffer sequence

$$\frac{\partial }{\partial x} L_n = \left(\frac{\partial }{\partial x}-1\right)L_{n-1}$$

Which can be rewritten as :

$$L_{n-1} = \frac{\partial }{\partial x}(L_{n-1}-L_n)$$

So by the fundamental theorem of calculus we can say

$$\int_0^xL_{n-1}(t)dt = L_{n-1}(x)-L_n(x)$$

So your sum is a pairwise sum of such integrals.

Remains to be proven that sum of such integrals for even $n-1$ are positive.

mathreadler
  • 26,534