Why combining two quadratic equations of a circle and a parabola creates extra solutions for $x$

Question

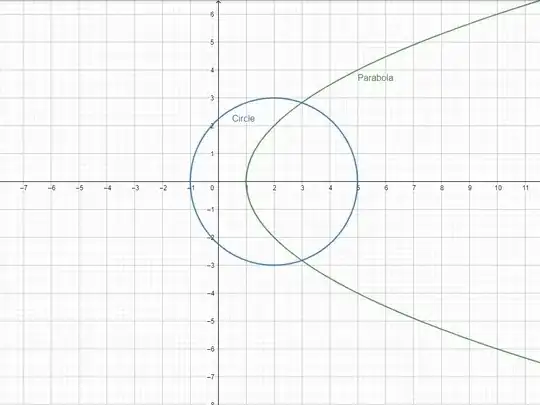
We have a parabola and a circle with the following equations and their graph placed at the end of my question.

Parabola: $y^2 = 4x -4$

Circle: $(x-2)^2 + y^2 = 9$

My goal was to calculate their intersection points so I substituted $y^2$ from the parabola equation into the circle equation and I got

$(x-2)^2 + (4x-4)=9 \implies x^2 - 4x + 4 + (4x - 4) = 9 \implies x^2 = 9 \implies x = \pm3$

$x=3$ is the only correct solution but why is $x=-3$ produced as an extra invalid solution?

What is the exact mathematical explanation behind this? Why substituting one equation into the other has produced extra answers?

update

When I calculate $x$ from the parabola equation and substitute it in the circle equation, I don't get any extra answers for $y$:

$y^2=4x-4 \implies y^2 +4 = 4x \implies x = \frac{y^2}{4} + 1$

$(x-2)^2 +(4x-4)=9 \implies ((\frac{y^2}{4} + 1) - 2)^2 + (4x - 4)=9 \implies y^4 +8y - 128 = 0 \implies y^2=8,-16$

$y^2 = -16$ cannot be true so $y^2 = 8 \implies y=\pm 2\sqrt{2}$ and these are correct answers for $y$.

2nd update

I made a mistake in the calculation in the previous update although the final solutions where correct. I write the correct calculation:

$(x-2)^2 +y^2=9 \implies ((\frac{y^2}{4} + 1) - 2)^2 + y^2=9 \implies (\frac{y^2}{4} - 1)^2 + y^2=9 \implies (\frac{y^4}{16} - \frac{y^2}{2} + 1) + y^2=9 \implies \frac{y^4}{16} + \frac{y^2}{2} + 1=9 \implies (\frac{y^2}{4} + 1)^2=9 \implies (\frac{y^2}{4} + 1)=\pm3 \implies \frac{y^2}{4} =2,-4 \implies y^2=8,-16$

Answer 1

Total there are 4 roots, two real roots you have given are ok. The remaining two with $x=-3$ substitution give imaginary $ y= \pm 4i$ and they should be discarded as extraneous, spurious etc. when looking for real solutions.

The above $x,y$ parts of a point should both be real for a full real solution.

$(x,y)= (-3,4i)$ are admissible as complex roots.

Had you computed $y$ values instead of $x,$ you would have noticed different imaginary values , with different signs as above.

Answer 2

When you are searching for intersection of two figures the intersection dot must satisfy parabola equation which indicates that

$$ y^2 = 4x - 4$$

Which means that

$$ 4x - 4 \geq 0$$ $$ x \geq 1 $$

The last inequality will exclude $x = -3$ solution.

Answer 3

$$(x-2)^2 + y^2 = 9 \tag{A}$$ requires that $x \in [-1,5]$ and $y \in [-3,3]$.

$$y^2 = 4x-4 \tag{B}$$ requires that $x \in [1, \infty)$.

So, for $x$ to satisfy both (A) and (B), we must have $x \in [1, \infty) \cap [-1,5] = [1,5]$.

Hence $x=-3$ will be an extraneous root.

Answer 4

I suppose that we are working on the real number system and not consider complex numbers but I think my reasoning works in complex numbers too. We want to solve a system of equations containing two equations. I move all terms of each equation to one side and name them $A(x,y)$ and $B(x,y)$

$\begin{cases} A(x,y)=y^2 -4x +4=0\\ B(x,y)=y^2 +(x-2)^2-9=0\\ \end{cases}$

We want to find tuples like $(x', y')$ such that $A(x',y')=0$ and $B(x',y')=0$ simultaneously.

If we calculate $y^2$ from $A(x,y)=0$ and substitute it into $B(x,y)$ we arrive at a third equation $C(x)=0$

$C(x) = 4x-4 +(x-2)^2-9 = 0 \implies C(x) = x^2 -9=0$

And when we solve $C(x) = 0$ we get $x^2=9 \implies x=\pm 3$ but any point $(-3,y)$ with $y\in\mathbb{R}$ does not satisfy $\begin{cases} A(x,y)=0\\ B(x,y)=0\\ \end{cases}$ and the solving procedure has produced extraneous solutions. The reason is this the line of reasoning is not reversible.

$\begin{cases} A(x,y)=0\\ B(x,y)=0\\ \end{cases} \overset{1}{\implies} C(x)=0 \overset{2}{\iff} x=\pm 3$

The $\overset{1}{\implies}$ is not reversible. In this case when there exists $(x_0,y_0)$ as a solution to the system we will have:

$\begin{cases} A(x_0,y_0)=0\\ B(x_0,y_0)=0\\ \end{cases} \overset{3}\implies C(x_0)=0 \overset{4}\iff x_0=\pm 3$

but if there exits $(x_1,y_1)$ as a solution to $C(x) = 0$ we will have

$C(x_1)=0 \;\not\!\!\!\implies \begin{cases} A(x_1,y_1)=0\\ B(x_1,y_1)=0\\ \end{cases}$

When we combine the equations we loose information and cannot retrive the system $\begin{cases} A(x_1,y_1)=0\\ B(x_1,y_1)=0\\ \end{cases}$ from $C(x)=0$ so every solution to the system is a solution to $C(x)=0$ but we cannot say every solution to $C(x)=0$ must be a solution to the system and extraneous solutions might have been produced.

Answer 5

A standard Cartesian graph deals only with real numbers "plotted against" real numbers, so in looking at the intersections of two curves in such a graph, one may not be "getting the whole story." Two distinct quadratic curves will have four intersections; since one of these (the circle) is bounded, all of the intersection points will be at finite distances from the origin.

If we use the curve equations with complex numbers $ \ x \ = \ a + bi \ $ and $ \ y \ = \ c + di \ \ , $ (with $ \ a \ , \ b \ , \ c \ , \ d \ $ real), they become $$ (x-2)^2 \ + \ y^2 \ \ = \ \ 9 \ \ \rightarrow \ \ ( \ [a - 2] + bi \ )^2 \ + \ ( \ c \ + \ di \ )^2 \ \ = \ \ 9 $$ $$ \rightarrow \ \ [ \ (a^2 - 4a - b^2 + 4) \ + \ (2a - 4 )·b·i \ ] \ + \ [ \ (c^2 - d^2) \ + \ 2cd·i \ ] \ \ = \ \ 9 \ + \ 0·i \ \ ; $$ $$ y^2 \ \ = \ \ 4x \ - \ 4 \ \ \rightarrow \ \ (c + di)^2 \ \ = \ \ 4·(a + bi) \ - \ 4 \ \ = \ \ (4a - 4) \ + \ 4bi \ \ . $$

The calculation without the imaginary parts ($ \ b \ = \ d \ = \ 0 \ $) is the one you made (the one we learn to make in "standard" analytic geometry), giving $ \ \ a^2 \ = \ 9 \ \ , \ \ c^2 \ = \ 4·a - 4 \ \ . $ We take $ \ a \ = \ +3 \ \ , $ $ c^2 \ = \ 4·(+3) - 4 \ = \ 8 \ \ , $ and "discard" $ \ a \ = \ -3 \ $ , since it leads to $ \ c^2 \ = \ 4·(+3) - 4 \ = \ -16 \ \ $ , which is not permissible since $ \ c \ $ is taken to be a real number. Your graph then represents real part $ \ c \ $ for $ \ y \ $ as a function of real part $ \ a \ \ $ for $ \ x \ \ . $

But a "graph" using complex numbers needs to be made in $ \ \mathbb{C}^2 \ \ , $ which can be interpreted in $ \ \mathbb{R}^4 \ \ , $ making it challenging to visualize, as the "curves" are then treated as four-dimensional. The intersections we "rejected" occur in those extended parts of the curves. If we return to the curve equations and work with the two-dimensional "slice" that "graphs" the imaginary part $ \ d \ $ of $ \ y \ $ against the real part $ \ a \ $ of $ \ x \ \ $ (so $ \ b \ = \ c = \ 0 \ $ ) , we obtain $$ ( \ [a - 2] + 0·i \ )^2 \ + \ ( \ 0 + di \ )^2 \ \ = \ \ 9 \ \ \rightarrow \ \ (a - 2)^2 \ - \ d^2 \ \ = \ \ 9 \ \ ; $$ $$ (0 + di)^2 \ \ = \ \ 4·(a + 0·i) \ - \ 4 \ \ \rightarrow \ \ -d^2 \ \ = \ 4a \ - \ 4 \ \ . $$

This produces $ \ a^2 \ = \ 9 \ \ , \ \ -d^2 \ = \ 4a - 4 \ \ , $ but using $ \ a \ = \ +3 \ $ will give us $ \ -d^2 \ = \ 8 \ \ , $ which we now "reject" because $ \ d \ $ is a real number; here, we take $ \ a \ = \ -3 \ \Rightarrow \ -d^2 \ = \ -16 \ \Rightarrow \ d \ = \ \pm 4 \ \ . $ As we see on the graph of $ \ d \ $ versus $ \ a \ $ below, we have found that a hyperbolic part of $ \ (x-2)^2 + y^2 \ = \ 9 \ $ intersects a parabolic part of $ \ y^2 \ \ = \ \ 4x \ - \ 4 \ $ at the points $ \ (-3 \ , \ \pm 4i) \ \ , $ as mentioned by Narasimham.

We have accounted then for the four intersections of the two curves, two of which are "invisible" on a "standard" graph in $ \ \mathbb{R}^2 \ \ . $ No other intersections appear on other "slices": for instance, the imaginary part $ \ d \ $ versus imaginary part $ \ b \ $ equations are $$ ( \ [0 - 2] + b·i \ )^2 \ + \ ( \ 0 + di \ )^2 \ \ = \ \ 9 \ \ \rightarrow \ \ 4 \ - \ b^2 \ - \ d^2 \ \ = \ \ 9 \ \ \rightarrow \ \ b^2 \ + \ d^2 \ \ = \ \ -5 \ \ ; $$ $$ (0 + di)^2 \ \ = \ \ 4·(0 + b·i) \ - \ 4 \ \ \rightarrow \ \ -d^2 \ \ = \ 4bi \ - \ 4 \ \ , $$ which do not produce real solutions for $ \ b \ $ and $ \ d \ \ . $