15

"Math lotto" is played as follows: a player marks six squares on a 6x6 square. Then six "losing squares" are drawn. A player wins if none of the losing squares are marked on his lottery ticket.
1)Prove that one can complete nine lottery tickets in such a way that at least one of them wins.
2)Prove that this is not possible with only eight tickets.

My attempt is as follows;

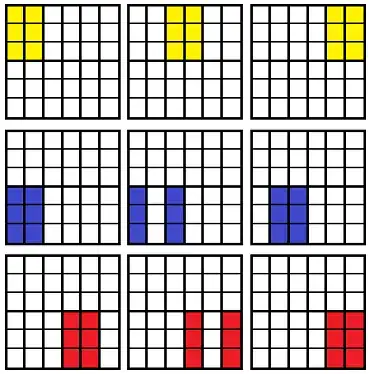
enter image description here First I divided the square into 6 rectangles (figure 1).
If one rectangle doesn't contain a cross then some ticket (ticket 1 to ticket 6) would win the game.

Now we consider the case where each rectangle has one cross each.
Now take the two rectangles on the top left of the square (figure 2). These have a total of two crosses.
The first two columns together contains one cross and the third and fourth columns together contains one cross.
There are four cases and we need at least four tickets (ticket 7 to ticket 10) to ensure win.

I am only getting a minimum of ten tickets. How do I prove only nine tickets is required and for eight tickets it is not possible?

Reference: Combinatorics by Stephan Wagner, Page 42, Problem 49 . https://math.sun.ac.za/swagner/Combinatorics.pdf

Joffan
  • 40,356
Asher2211
  • 3,416

2 Answers2

12

Just to provide a concrete choice of 9 tickets that will have at least one winning ticket:

enter image description here

Suppose to the contrary that all of these are losing tickets. The yellow ones forces 3 losing squares on the top half. Then 3 remaining losing squares will fill the bottom half. By pigeonhole, at least 2 of these losing squares will be in the bottom left 3x3 or the bottom right 3x3.

Say there are at least two losing squares in the bottom left 3x3, which means at most 1 losing square is in the bottom right 3x3. In this case one of the red tickets will not have a losing square, as the losing square is in one of the 3 columns.

And vice versa, if at least two losing squares are in the bottom right 3x3, then one of the purple tickets will not have a losing square.

Edit. A reference for this problem can also be found here https://www.cut-the-knot.org/pigeonhole/MathLotto.shtml

bonsoon
  • 3,109
  • 3
    Put more simply, it takes at least three losing squares to sink the yellow tickets, at least two more for red, and at least two more for blue. That's seven total, but we've only got six. – Misha Lavrov Jan 23 '21 at 01:35
  • That's how I thought of it originally, like the game battleship. – bonsoon Jan 23 '21 at 01:56
8

Here is a proof that, given a set of 8 tickets, we can always find 6 losing squares such that each ticket has marked at least one losing square.

If there is a square that is marked on 3 tickets, we choose that square along with one square from each of the other 5 tickets to be losing. So suppose instead that each square is marked on at most 2 tickets. By the pigeonhole principle, there must be a square marked on exactly two tickets; call it Square A. The remaining 6 tickets avoid square A, so applying the pigeonhole principle again, there must be a different square marked on two of the remaining 6 tickets; call it Square B. As losing squares, we then choose Square A, Square B, and one square from each of the remaining 4 tickets.

A very similar argument can prove that, if we have a collection of 9 tickets with the property that at least one will be a winner, then no square can be marked on 3 or more of those tickets.

Julian Rosen
  • 16,600