16

In one of his books, Peter Winkler includes the following problem:

A disease is spreading on a $n\times n$ chessboard as follows: if a healthy cell is neighboring at least 2 infected cells, it becomes infected. Using the property that the perimeter of the infected area never increases, it’s easy to prove that it’s impossible to infect the entire chessboard with fewer than $n$ infected cells.

If the chessboard is a torus, the result no longer holds (verified on some instances of $n$). It seems that $n-1$ is the smallest number of infected cells required to infect the chessboard. The perimeter argument can’t be used here. Does anyone know any other ‘invariant’ that can be used?

Note: two cells are neighbors if they share one side.

user2471
  • 403
  • Are cells that share only a common vertex considered to be neighbors, or is it only cells that share a side that are neighbors? – Paul Sinclair Jan 17 '21 at 15:43
  • 1
    Never mind - obviously you are only allowing cells with shared sides to be neighbors. Otherwise the non-increasing perimeter property would be false. It holds because each new infected cell removes the borders it shares with its two infecting neighbors from the perimeter, and can only add at most its other two sides to the perimeter. – Paul Sinclair Jan 17 '21 at 15:59
  • @PaulSinclair to be precise, a newly infected cell removes at least 2 edges and adds at most 2. – user2471 Jan 17 '21 at 16:59
  • 1
    If you draw a rectangle around a collection of infected cells, they will never escape that rectangle unless there are other infected cells within a distance of $2$ from it. For a torus of diameter $n$ and only $n-2$ starting cells, you can try to show that the starting cells can always be encased in independent rectangles that do not cover the entire torus. – Paul Sinclair Jan 17 '21 at 19:35
  • @PaulSinclair I think if we can prove that any n-2 cells necessarily belong to an (n-1)x(n-1) sub-grid of the torus, then we’re done. It may just be a combinatorial argument at this point. I was hoping for an invariant type of argument similar to the perimeter for the non modular case. I tried to reason with a notion of ‘diameter’ of the infected area, but I didn’t get far :-) – user2471 Jan 18 '21 at 02:56
  • 1
    For a torus, you need to trap it in an $n-2$ strip in at least one direction. If it extends to a width of $n-1$, then it will be in reach of its own other side, and fill that final strip. – Paul Sinclair Jan 18 '21 at 03:41
  • @PaulSinclair you’re right. I miss typed in my previous comment. I meant (n-2)x(n-2) sub grid. – user2471 Jan 18 '21 at 05:58
  • 3
    Crossposted to MO: https://mathoverflow.net/questions/381576/spread-of-a-disease-on-a-modular-chessboard-torus-lower-bound – Qiaochu Yuan Jan 19 '21 at 00:16
  • 1
    @QiaochuYuan: Also recently asked on puzzling.SE: https://puzzling.stackexchange.com/questions/106444/infected-cylinder-and-torus – Ilmari Karonen Jan 19 '21 at 00:42
  • 2
    Unfortunately, the strategy user2471 hoped for can't work; consider the 4 by 4 torus with (0, 0) and (2, 2) infected - any 2 by 2 square will miss one of the infected squares. – user44191 Jan 19 '21 at 00:53
  • @user44191 Yep! What I stated sounded too comforting to be true :-) I realised almost immediately after I added my comment. – user2471 Jan 22 '21 at 01:48
  • This is problem 66 in Béla Bollobás, The Art of Mathematics, CUP 2006. – darij grinberg Feb 08 '21 at 00:17

2 Answers2

4

EDIT: This answer is actually totally wrong! I'm leaving it up so that others do not make the same mistake as I, but here is an example (thanks to Anton Petrunin) which shows that my supposed non-increasing quantity actually can increase. Initially, three cells are infected, and the restricted perimeter is $10$, but after 3 moves, the restricted perimeter increases to $12$.

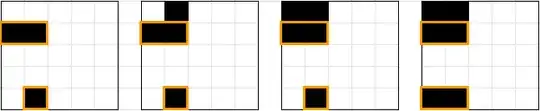
enter image description here

Suppose there are only $n-2$ infected cells. Without loss of generality, these infected cells occur in the lower left $(n-1)\times (n-1)$ subgrid of the torus. If not, rotate the torus until one of the columns with no infections is on the right (such a column must exist, since there are at most $n-2$ infections), then rotate until a row with no infections is on top.

The desired invariant quantity is the perimeter of the figure comprising the infected cells only in the lower left $(n-1)\times (n-1)$ subgrid, ignoring wrap-around. Let us call this the "restricted perimeter."

To prove invariance, note that a cell which becomes infected in the top row or right column does not affect the restricted perimeter at all. On the other hand, a cell in the lower left $(n-1)\times (n-1)$ subgrid becoming infected does not increase the restricted perimeter for the same reason as in the non-torus case.

With this definition, the same argument goes through. If there are initially $n-2$ infected cells, then the restricted perimeter is at most $4(n-2)$. But when if the entire torus is infected, the restricted perimeter would be $4(n-1)$.

Here is an example when $n=4$. The left grid is the initial infection, with two infected cells. The restricted perimeter is initially $8$. The right grid is the infection one step later, and the restricted perimeter is still $8$. The edges contributing to the restricted perimeter are highlighted in orange. The topmost orange edge in the second picture might appear strange, since it is between two black squares. But remember, you have to mentally delete the top row and right edge, then consider the perimeter of what remains.

enter image description here

Mike Earnest
  • 84,902
  • Just to elaborate on why the square argument goes through for the $(n-1)\times (n-1)$ grid but not the torus itself: if we cut out a row and column from the torus, what we have left has no wrap-around, so we really are dealing with a square in terms of the adjacencies of different cells. – RavenclawPrefect Jan 19 '21 at 23:04
  • 3
    If you start with 3 cells (1,4), (2,4), and (2,1) on a 5x5-torus, then restricted perimeter increases on the step 3. – Anton Petrunin Jan 20 '21 at 00:04
  • I tried similar approach and that’s why I gave up on the perimeter as an invariant. Thanks for keeping this as a reference. – user2471 Jan 20 '21 at 21:29
  • I do not see why your answer is wrong? In your "EDIT", simply WLOG shift the rows up, twice. Then, it is clear we simply have a 3 by 2 rectangle which still has perimeter 10, in your lower left subgrid (WLOG somewhere on the torus). – Vepir Jan 25 '21 at 15:01
  • @Vepir Please read the quoted definition in the body of my post. I had claimed a novel concept called "restricted perimeter" was non-increasing, I was not talking about perimeter. – Mike Earnest Jan 25 '21 at 15:46
  • @MikeEarnest I was talking about "restricted perimeter", it does not increase? Slide and or rotate the grid on the torus to get a 3 by 2 rectangle in the "lower left subgrid" - as seen in this illustration, red grid is equivalent to the blue grid. . – Vepir Jan 25 '21 at 16:23
  • Oh, I think I only now realize what exactly was meant by your "restricted perimeter". The (n-1) by (n-1) subgrid is constant and selected before the infection spread. Now the EDIT makes sense. My bad. – Vepir Jan 25 '21 at 19:34
1

Consider separately two ways the infection can grow. When infection spreads to an empty cell, it can be that two of the adjacent infected cells share a corner (which is always the case when there are three or four adjacent infected cells) or not, in which case the two infected cells are both in the same row or column.

Within a row or column, we will say a component is a group of consecutive infected cells in that row or column. (We don't care whether the infected cells are connected via a path that lies outside the row or column.) Our proposed invariant is based on the total number of components among both rows and columns (with an exception noted below).

We will consider growth not in generations, but in individual steps where the infection grows to only a single cell at each step. (The order will not matter unless noted.)

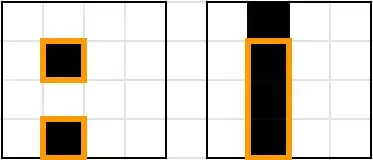
Under the first kind of growth, new components cannot be created. The step can only decrease the number of components in a row or column or both.

Under the second kind of growth, usually the number of components of a single row or column will go down by one (as the components are joined by the infection of the cell between them) and the number of components in the corresponding column or row will either increase by one or stay the same. In this case, then, the total number of components will not increase.

The other case is when the last cell in the row or column is being infected. The first time this happens for rows and the first time for columns, it can indeed increase the number of components by one. However, we not need to concern ourselves with subsequent times. Without loss of generality, consider rows. If one row is already completely infected and a second row is one cell from being completely infected, then either there is a column component that connects these row components or not. If there is a connecting column component, then (by infecting in a different order) the first kind of growth can be used to infect the entire stripe bounded by the rows and the connecting component. (This includes the last cell in this new row which will have been infected without increasing the number of components.) If there is no such connection, then in $n - 1$ columns, there are at least $2$ components each plus at least $1$ component in the last column plus $2$ rows with at least one component. This is at least $2n + 1$ total components. We will not be concerned with cases that have so many components.

If we start with $n - 2$ infected cells, then there are at most $n - 2$ column components and $n - 2$ row components for a total of $2n - 4$ components. At most two new components can be introduced; one by the first full row infection and one by the first full column infection. This gives at most $2n - 2$ components. As this is less than $2n + 1$, any subsequent full row or column infection can be completed by growth of the first kind without increasing the number of components. Thus, the final number of components will be at most $2n - 2$. This is less than the $2n$ of the completely infected board.

tehtmi
  • 1,083
  • Notice this is very similar to the perimeter invariant. Horizontal contributions to the perimeter are like boundaries between column components and vertical contributions are like boundaries between row components. – tehtmi Jan 27 '21 at 13:03
  • 1
    Very nice! In effect, the non-increasing quantity is perimeter/2 + # completed rows + # completed columns. This quantity can increase by 1 at most twice, when the first row and columns is completed; for any further increases, the infection order can be changed to eliminate them. – Mike Earnest Feb 02 '21 at 19:53