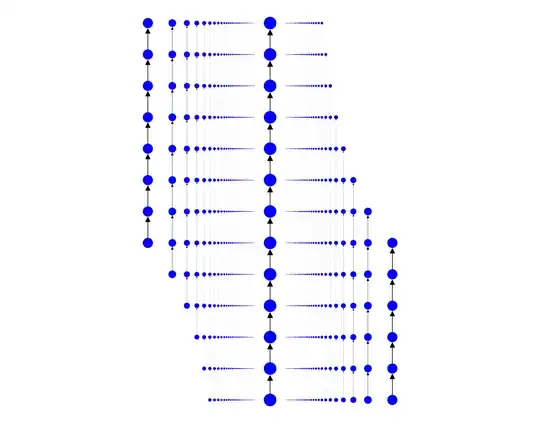
I think both of the examples given at mathoverflow are actually covering maps.
I claimed in the comments that I had a somewhat discrete example but I transformed it to a manifold-based example. The space $X$ is the Möbius strip and $G = ℤ$. I haven't found a really nice way of describing the action but I'll do what I can.
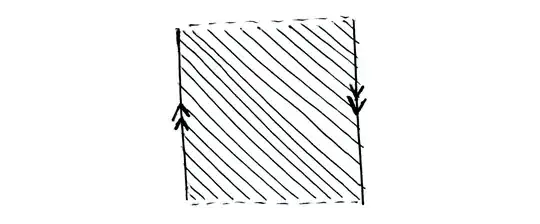
We start by describing a free action of $ℝ$ on $X$. The quotient is $[0,1[$ and the fibers of the quotient $X↠[0,1[$ are shown on the drawing below.
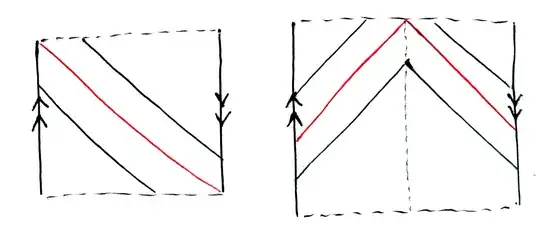
Notice that the "cut" chosen above to draw the Möbius strip above is special. If we displace the cut, we see an angle appear in the fibers. Below are other drawings of two of the fibers. The one in red is the fiber above $0 ∈ [0,1[$.
The action of $ℝ$ is done by "following the fibers" in a chosen direction, but you need to slow down more and more as you approach the angle of the red line. Maybe it's a bit hard to see that it works on the drawings I gave. Here is a different way of drawing the Möbius strip and the two fibers. Imagine it has an infinite height.
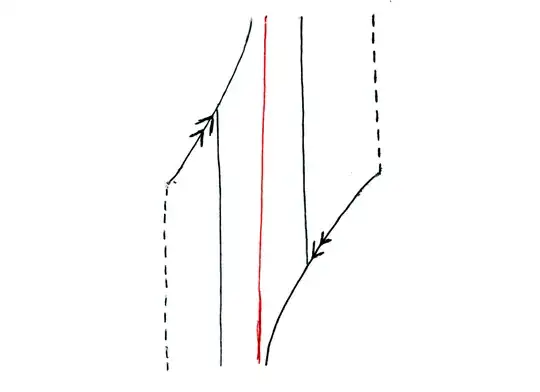
On this drawing, the action of $ℝ$ is isometric on the fibers and easier to see (translate along the $y$ direction and teleport to the other side of the red line when you end up out of the drawing).
To get an action of a discrete group and discrete orbits, we restrict the above action to $ℤ⊆ℝ$. The quotient becomes $[0,1[ × S^1$ and the quotient map is not a covering above $(0,x)$ for any $x ∈ S^1$.
To give you an idea of the initial "discrete" example I had, here is a drawing of it. I don't explain more, it's very similar to what I said above. I built by trying to contradict the properness of the action in the simplest way possible.