Problem 1.13 from Irodov's Problems in General Physics:
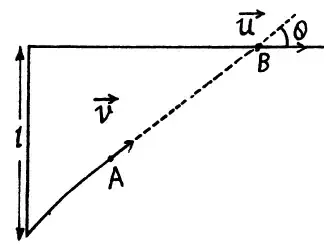
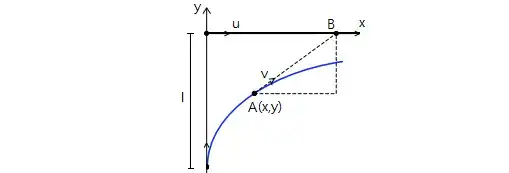
Point A moves uniformly with velocity $v$ so that the vector $v$ is continually "aimed" at point B which in its turn moves rectilinearly and uniformly with velocity $u<v$. Initially, $v⊥u$, and the points are separated by a distance $l$. The time at which the points converge is given as?
If we write $\tau$ as the time to collision, then we can immediately find
$$\int_0^\tau v\cos\theta\,dt=u\tau\Leftrightarrow\int_0^\tau\cos\theta\,dt=\frac{u\tau}{v}\\\int_0^\tau v\sin\theta\,dt=l\Leftrightarrow\int_0^\tau\sin\theta\,dt=\frac{l}{v}$$
Irodov asserts that
$$\int_0^\tau(v-u\cos\theta)dt=l$$
It turns out that if we consider $\vec w=\vec v-\vec u=(v\cos\theta-u,v\sin\theta)$, then $v-u\cos\theta$ is $v\cos\theta-u$ in the basis $(\hat v,\hat v_\perp)$, where $\hat v=(\cos\theta, \sin\theta)$ and $\hat v_\perp=(\sin\theta,-\cos\theta)$ in $(\hat\imath,\hat\jmath)$.
$\vec w=(v-u\cos\theta,-u\sin\theta)$ in $(\hat v,\hat v_\perp)$.
Consider integrating $\vec w$ (I use the integrals of the sine and cosine above in the process) $$\int_0^\tau\vec w\,dt=\left(\int_0^\tau(v\cos\theta-u)\hat\imath dt\right)+\left(\int_0^\tau(v\sin\theta)\hat\jmath dt\right)=l\hat\jmath$$ Now consider the same but with the coordinates in $(\hat v,\hat v_\perp)$ $$\int_0^\tau\vec w\,dt=\left(\int_0^\tau(v-u\cos\theta)\hat v dt\right)+\left(\int_0^\tau(-u\sin\theta)\hat v_\perp dt\right)=\left(\frac{v^2-u^2}{v}\tau\right)\hat v-\left(\frac{ul}{v}\right)\hat v_\perp$$ If we equate both integrals and take the norm squared, we get $$\left(\frac{v^2-u^2}{v}\tau\right)^2+\left(\frac{ul}{v}\right)^2=l^2\Leftrightarrow\tau=\frac{l}{\sqrt{v^2-u^2}}$$ But this is wrong, the actual value is $$\tau=\frac{vl}{v^2-u^2}$$ Can anyone spot the error? Thank you!