I thought about the parameterizing the 4D sphere using $$x_1= r\cos(\theta_1), x_2= r\sin(\theta_1)\cos(\theta_2), x_3= r\sin(\theta_1)\sin(\theta_2)\cos(\theta_3),\\ x_4= r\sin(\theta_1)\sin(\theta_2)\sin(\theta_3),$$ where $x_1,x_2,x_3,x_4$ are my 4D space coordinates. But what will be the range of values of $\theta_1, \theta_2, \theta_3$ to make the mapping from $(r,\theta_1, \theta_2, \theta_3)$ to $(x_1,x_2,x_3,x_4)$ bijective ?
Asked
Active
Viewed 65 times
0
-
1Your title is seemingly unrelated to your question. To construct a bijective mapping from a cuboid to a sphere, just inflate the cuboid until it becomes a sphere. You don't need spherical coordinates to do that. – Ivan Neretin Jan 08 '21 at 15:00
-
1Be careful - this is not the 4 sphere. It is the 3 sphere with radius $r$. – K.defaoite Jan 08 '21 at 15:53
1 Answers
2
I think the other commenters were too quick to disregard this question. I personally think that this question is interesting, so I'm going to give a hint.
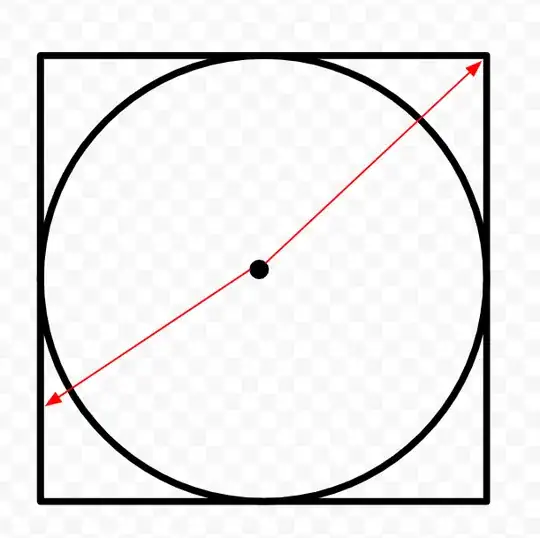
When dealing with higher dimensional geometry, it usually helps to start first on a low dimensional case and then work your way up. WLOG, I will assume the radius of the sphere we want to map to is $1$. The way we do this is to shoot out rays radially that intersect the box and the sphere. Here's a diagram of the one dimensional case:
Can you construct a bijective mapping that takes a point on the circle to a point on the sphere? Think about the line that goes through both points. How can we generalize this to more dimensions?
K.defaoite
- 13,890