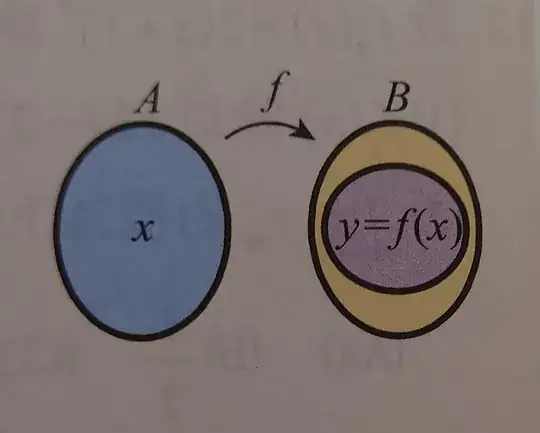7

I’m just a high school student, so I may be somewhat logically flawed in understanding this.

According to wikipedia, the definition of function requires an input $x$ with its domain $X$ and an output $y$ with its domain $Y$, and the function $f$ maps $x$ to $y$.

But how about $f(x)$? I often see syntaxes such as $f(1) = 0$ in my textbook. Doesn’t that mean it is $f(x)$ being first assigned a value and then transfer the value into $y$? So, there must be two transitions/mappings between the input $x$ and the output $y$ right?

My conceptual model of function is like this: A definition of function requires an input $x$ with its domain $X$, a forwarder $f(x)$ with its domain $F$ and an output $y$ with its domain $Y$. The function $f$ first maps $x$ to $f(x)$ then maps $f(x)$ to $y$.

These two definitions are not quite the same.

On 2022.6.29: The picture below had solved my confusion.

enter image description here

Timothy Chang
  • 71

5 Answers5

3

Equality is not just a mapping. It means two things are one and the same.

We wrote $f(x) = y$ not to indicate that we are mapping $f(x)$ to $y$; it means that $f(x)$ is $y$.

Consider a function $f$ that maps any value $x$ in the domain $\mathbb Z$ (the integers) to a value $y$ in the codomain $\mathbb Z$. (Codomain rather than domain is the correct word here.) In particular, $f$ is the function that maps each integer to the previous integer, so $f$ maps $3$ to $2$, $f$ maps $2$ to $1,$ and $f$ maps $1$ to $0.$

Then the notation $f(1)$ is simply a way of saying "the number that $f$ maps $1$ to." So if you ask, "What is $f(1)$," the answer is $0$, because $f$ maps $1$ to $0$.

Again: $f$ maps $1$ to $0$, therefore the number $f$ maps $1$ to is $0$; that is, $f(1)$ is $0$. We express this in the equation, $f(1) = 0$.

It is certainly possible to set up a situation in which a member of one set is mapped to something which is then mapped to something else. But that is not how a single function is defined. A function defines exactly one transition from one set to another, and the notation $f(x)$ is one way to express the final result of that transition. If $f$ maps from a domain $X$ to a codomain $Y$ then $f(x)$ is already a member of $Y$ and needs no further "transitioning" to get to $Y$.

Notice that in the previous paragraph I never mentioned any variable named $y$. Indeed I too take issue with the part of the Wikipedia article that says, "this relation is denoted by $y = f (x)$ ... where the element $x$ is the argument or input of the function, and $y$ is the value of the function ... ." The symbol $y$ is completely superfluous here; if we use $x$ to represent the input of the function, the usual denotation for the value of the function is $f(x)$, and a denotation that actually shows the relation of an element $x$ in the domain to an element in the codomain is $x \mapsto f(x).$ Here $f(x)$ is the element of the codomain and $\mapsto$ is the relation.

David K
  • 108,155
  • To summarize, (1) equality here doesn't mean a mapping, and an additional mapping is unnecessary (2) the relation can be simply described as $x \mapsto f(x)$ and $x \in X,, f(x) \in f(X) \subseteq Y$, which can be illustrated by the newly added picture in the OP's question. – Timothy Chang Jun 29 '22 at 08:29
1

We talk about domains and codomains of a function, not of the variables of a function. You might not have come across the term codomain before, but I think that it's the best for what you're trying to describe.

So, the domain of $f$ is $X$ and the codomain of $f$ is $Y$. Often, we write this as $f:X\rightarrow Y$ to indicate that the valid inputs to $f$ are points in $X$ and every output of $f$ is a point in $Y$.

In your example, $x$ is a point in $X$, which is the domain of $f$, and $y$ is a point in the codomain of $f$, which is $Y$.

Michael Burr
  • 33,866
  • y=f(x) means the y value is the output (dependent variable) of f given input x value (independent variable). y=ax+b does not indicate this type of domain-'codomain' relationship, though in causal two-variable equations (as contrasted with lesser correlations), the non-x one (y, t, etc) is typically treated as the output (particularly for non-invertible functions that aren't one-to-one) so its set of values (continuous or discrete, both or neither) represent the range, mapped from the domain of the dependent values (commonly x, same as horizontal axis) via function f. –  Jan 10 '21 at 03:19
1

The notation $f(1)=0$ means that $f$ maps $1 \in X$ to $0 \in Y$. This agrees with the familiar notation $y=f(x)$ form that most people encounter in high school such as $y=ax^2+bx+c$. This means that $f(x) \in Y$ is always true. There is no other assignment operation occurring. Alternatively if you define functions as a kind of relation $f \subset X \times Y$ then $f(1)=0$ means $(1,0) \in f$. In both cases it's merely two names of the same thing.

CyclotomicField
  • 11,925
  • 1
  • 14
  • 32
-1

I'm the OP, and I now kind of know what was causing me confusion back then.

I was actually thinking of function in a more computer science way. When we use the notation $y = f(x)$ in programming languages, it actually functions in the same way as I described in the question above. It first calculates $f(x)$ with the input $x$ and then stores the result into a temporary variable, and it then assigns the value of the temporary variable to the variable $y$. It does have two transitions in the process.

Yes, of course one can argue that function in mathematics doesn't need to have the same definition as function in programming languages. I agree, even though it is really weird to have two different definitions describing the same concept. But it is actually worthwhile to talk about which of them is more appropriate and more intuitive.

If we redefine function in mathematics in a more computer science way. We can define a function as $f: I → O$ , where $f$ maps the input $x$ in the domain $I$ to the output $f(x)$ in the codomain $O$. Defining function in this way makes a much more elegant expression, which would get rid of the redundant usage of $y$ which just means the same as $f(x)$. Confusion in choosing which notation to use happens all the time, not only in choosing between $f(x) = ax+b$ or $y = f(x) = ax+b$ but also $dy/dx$ or $df(x)/dx$.

Moreover, if we look back to the definition of function in programming languages, this kind of redundancy just doesn’t exist at all, and it never caused any problem. The variable $y$ is not pre-defined in the function itself, and is actually only needed when we want to “store” the final result, not to “use” the result for further calculation. The “real” output of the function $f$ is $f(x)$, not $y$.

The variable y can still be used with function in mathematics, but now it should no longer be seen as part of the definition of function. The expression $y = f(x) = ax+b$ thus should be understood alternatively as simultaneous equations of $y=f(x)$ and $f(x) = ax+b$.

To conclude, I think the original definition is obviously outdated and flawed compared to the more modern one used in computer science. It deserves a refurbished definition as it has been a quite fundamental and frequently used concept in mathematics, hopefully urgently.

Timothy Chang
  • 71
  • 1
    A function is defined in mathematics in your proposed "computer science" way; see here. The issue here is the notation, which is sort of doing multiple things at once in an annoying way. But there's no need to update the notion of function, since it's already what you describe. – Noah Schweber Jan 12 '21 at 18:23
  • Really? I thought I am the only one who is annoyed with these notation stuffs and others are having no trouble using these confusing notations... I’ll look into the post you linked, thanks a lot! – Timothy Chang Jan 12 '21 at 18:32
  • I personally found it annoying when I was first learning about functions and algebra. But it quickly gets better with practice. – Noah Schweber Jan 12 '21 at 18:34
  • I think the point of confusion here is that y = f(x) in a typical C-like computer language is not the same thing as $y = f(x)$ in mathematics. Even y = 1 is complicated; it says that before this expression is executed, y stores some value which might not be 1, but after the expression is executed it stores 1. In a language with C-like expressions, (y=1)&&(y=0) is a perfectly well-defined expression that will (in the end) result in storing the value 0 in y, but mathematically $y=1 \land y=0$ implies $1=0$, which is a contradiction. – David K Jan 13 '21 at 12:43
  • Note that $1=y$ is a perfectly OK thing to write mathematically, but 1 = y in a C-like language will result in a compile-time error. Also note that some computer languages use other symbols for assignment; in such a language, = might just be a comparison operator; y = f(x) and f(x) = y might have the same meaning and might simply evaluate to "true" if y already stores the same value that f(x) produces, but neither expression would change the value stored in y. – David K Jan 13 '21 at 12:50
  • By the way, if you want to really talk about computer science, there is an entire subject within computer science on the theory of computer languages, in which the semantics of assignment (y = 1 in a C-like language) is analyzed. Refer to the linked chapter on Denotational Semantics: it takes 21 pages (page 291 of the book) to get to a point where it is ready to describe the assignment operator (which it calls := in the Pascal tradition rather than = in the C tradition). – David K Jan 13 '21 at 13:37
  • Also by the way, I finally looked in the Wikipedia article to find the part you were quoting from. Indeed the way that particular part of the Wikipedia entry is written is problematic. Wikipedia is a fine place to go to get ideas to follow up on, but it's not a good source to rely upon for fundamental definitions. – David K Jan 13 '21 at 13:47
-2

I see what you are saying, but there are ways to think about this without using more than one mapping, as the other answers have pointed out.

But here is what I think you are getting at (which I agree with):

$x \mapsto f(x) \mapsto ax+b$. where we have a general function of $x$ and we send it to some expression in terms of the variable $x$.

Then $x$ maps to $f(x)$ as normal by using the domain and codomain.

Derek Luna
  • 2,869
  • 4
    The second $\mapsto$ seems to signify that $ax+b$ is something different from $f(x).$ It looks like some kind of composition of functions where the second-applied function has the rule $u \mapsto af^{-1}(u) + b$ (provided the function $f$ is invertible; otherwise the second $\mapsto$ doesn't make sense). I think this answer is likely to be misleading. – David K Jan 10 '21 at 02:45
  • 1
    @David K In general, $f(x)$ on its own is something different, until one defines it. That is what OP is asking about. I don't personally think of $f(x)$ only meaning something once it is defined in a problem. I think of it on its own until we define it by sending it to some expression containing the variable $x$. This is how I think about it anyway. Similar to how $x$ is a placeholder for values, $f(x)$ is a placeholder for $x$-variable expressions, and defining that creates another mapping (in my mind). – Derek Luna Jan 10 '21 at 02:49
  • 1
    You can certainly use $f$ as a symbol for a general function or for some function that you are going to define later but have not yet defined. The notation $f(x)\mapsto ax+b$ is still misleading. And in any case a function maps an element from its domain directly to something in its codomain, even if we haven't yet decided what the domain, codomain, and mapping will be; there is no time at which it makes sense to talk of $f(x)$ as something that is not a member of the codomain of $f$ and not simply the value that $f$ maps $x$ to. – David K Jan 10 '21 at 02:55
  • I guess we will just have to disagree then. – Derek Luna Jan 10 '21 at 02:55
  • 3
    So are you saying that $f(x)$ is not a member of the codomain of $f$ and is not simply the value that $f$ finally maps $x$ to? (I think maybe you do not mean to say that, because when I look at the last sentence of your answer it seems to say $f(x)$ is the member of the codomain of $f$ that $f$ maps $x$ to.) – David K Jan 10 '21 at 02:57
  • 1
    The variable $x$ maps to a general function $f(x)$ , but also the general function $f(x)$ maps to the expression $ax+b$ by our definition so that there is a composite mapping from $x$ to $ax+b$ which perhaps CAN be described simply by $f$ and its defined rule.This is how I think about it, and I answered because I believe it is just as valid. – Derek Luna Jan 10 '21 at 03:12