Application of Induction in the analyze of the convergence a sequence defined recursive.

Question

Let $\left\{a_{n}\right\}$ be defined recursively by $$ a_{n+1}=\frac{1}{4-3 a_{n}}, \quad n \geq 1 $$ Determine for which $a_{1}$ the sequence converges and in case of convergence find its limit.

My approach: Note that $$a_{n +1}=\frac{1}{4-3a_{n}}, \quad n\geq 1$$ so, firstly I would like to find $a_{n}$. Now, I was trying to find a pattern but I can't find this \begin{eqnarray*} n=1 &\implies & a_{2}=\frac{1}{4-3a_{1}}=\frac{(3^{2-1}-1)-(3^{2-1}-3)a_{1}}{(2^{2})-(3^{2}-6)a_{1}}\\ n=2 & \implies & a_{3}=\frac{1}{4-3a_{2}}=\frac{1}{4-3 \left( \frac{1}{4-3a_{1}}\right)}=\frac{4-3a_{1}}{4(4-3a_{1})-3}\\ \vdots &\implies & \vdots \\ \end{eqnarray*} If I know $a_{n}=a_{n}(a_{1})$, so I can analyze the denominator for the conclude when $a_{n}$ is not defined.

How can find $a_{n}$?

Also I know this problem was answered here. But I think, we can find an elementary solution using induction on $n$.

Answer 1

If the sequence converges to $L$, taking the limit on both sides of the recurrence shows that

$$L=\frac1{4-3L}\,,$$

or $3L^2-4L+1=0$. The quadratic factors nicely: $(3L-1)(L-1)=0$, so the only possible limits are $L=\frac13$ and $L=1$.

Clearly the sequence is undefined if $a_1=\frac43$ and constant if $a_1=\frac13$ or $a_1=1$.

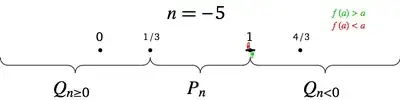
• If $a_k<1$, then $1<4-3a_k$, and $0<a_{k+1}<1$.
• If $a_k>\frac43$, then $a_{k+1}<0$, so $0<a_{k+2}<1$.
• If $1<a_k<\frac43$, let $r=a_k-1$; then $0<3r<1$, so $$a_{k+1}=\frac1{4-3a_k}=\frac1{1-3r}=\sum_{n\ge 0}(3r)^n>1+3r>a_k\,.$$ The sequence cannot have a limit in $\left(1,\frac43\right]$, so either it hits $\frac43$ and dies, or $a_\ell>\frac43$ for some $\ell>k$, and then $a_n\in(0,1)$ for all $n\ge\ell+2$.

Thus, if $a_1$ actually generates an infinite, non-constant sequence, that sequence ends up in $(0,1)$. What happens there?

• If $\frac13<a_k<1$, let $r=a_k-\frac13$. Then $$a_{k+1}=\frac1{4-3a_k}=\frac1{3(1-r)}=\frac13\sum_{n\ge 0}r^n\,,$$ so $$a_{k+1}-\frac13=\frac13\sum_{n\ge 1}r^n=\frac{r}3\sum_{n\ge 0}r^n=ra_{k+1}<r=a_k-\frac13\,,$$ and $a_{k+1}<a_k$. In this case the sequence must converge to $\frac13$.
• If $0<a_k<\frac13$, let $r=\frac13-a_k$. Then $$a_{k+1}=\frac1{4-3a_k}=\frac1{3(1+r)}=\frac13\sum_{n\ge 0}(-1)^nr^n\,,$$ so $$\begin{align*}\frac13-a_{k+1}&=\frac13-\left(\frac13+\frac13\sum_{n\ge 1}(-1)^nr^n\right)=\frac13\sum_{n\ge 0}(-1)^nr^{n+1}\\&=\frac{r}3\sum_{n\ge 0}(-1)^nr^n=ra_{k+1}<r=\frac13-a_k\,,\end{align*}$$ and $a_{k+1}>a_k$. Again the sequence converges to $\frac13$.

We have now shown that $a_1=1$ yields the constant sequence $a_k=1$ for all $k\ge 1$, and every other initial value yields either a sequence converging to $\frac13$ or one that eventually dies because some $a_k=\frac43$. It only remains to determine for which initial values some $a_k=\frac43$.

Solving $y=\frac1{4-3x}$ for $x$, we find that $x=\frac{4y-1}{3y}=\frac43-\frac1{3y}$. Let $b_1=\frac43$, and for $k\ge 1$ let $b_{k+1}=\frac{4b_k-1}{3b_k}$. It’s easy to show by induction on $k$ that $a_k=\frac43$ if and only if $a_1=b_k$, so $\{b_k:k\ge 1\}$ is the set of initial values that do not yield a convergent sequence, and it only remains to find a closed form for the numbers $b_k$.

If we write $b_k$ as a fraction $\frac{c_k}{d_k}$, then

$$b_{k+1}=\frac{\frac{4c_k}{d_k}-1}{\frac{3c_k}{d_k}}=\frac{4c_k-d_k}{3c_k}\,,$$

so $c_{k+1}=4c_k-d_k$, and $d_{k+1}=3c_k$, with initial conditions $c_1=4$ and $d_1=3$. Then $c_{k+1}-d_{k+1}=c_k-d_k$, so by induction $c_k-d_k=c_1-d_1=1$ for all $k\ge 1$. It follows that $c_{k+1}=d_{k+1}+1=3c_k+1$. Solving the recurrence $c_{k+1}=3c_k+1$ with initial value $c_1=4$ by any standard method, we find that

$$c_k=\frac{3^{k+1}-1}2$$

and hence that

$$d_k=\frac{3^{k+1}-3}2\,,$$

so that

$$b_k=\frac{3^{k+1}-1}{3^{k+1}-3}\,.$$

Answer 2

Update: Thanks Brian M. Scott for your insight.

I'll add the case where some $a_k=\frac 43$. Per Brian, we need to solve for the sequence $b_k$ such that $b_1=\frac 43$, $b_{k+1}=\frac{4b_k-1}{3b_k}$. This can be solved in a similar fashion, but easier because $b_1$ is given.

Note that $$ b_{k+1} - 1 = \frac{b_k-1}{3b_k}$$$$ b_{k+1} - \frac 13 = \frac{b_k-\frac{1}{3}}{b_k}\tag 1 $$

From $(1)$ we conclude $b_k>\frac 13, \forall k$ via induction.

Then $\frac{b_{k+1}-1}{b_{k+1}-\frac 13} = \frac{1}{3} \frac{b_k-1}{b_k-\frac 13} \implies \frac{b_k-1}{b_k-\frac 13} = \frac{1}{3^{k-1}} \left( \frac{b_1 - 1}{b_1 - \frac 13}\right) = \frac{1}{3^k}$

Therefore $b_k = \frac{1 - \frac{1}{3^{k+1}}}{1-\frac{1}{3^l}} = \frac{3^{k+1} -1}{3^{k+1}-3}$ which is the same as Brian's results.

---

Original answer:

Since $1$ and $\frac 13$ are roots of the characteristic equation $x=\frac{1}{4-3x}$, we have

$$a_{n+1}-1 = \frac{3(a_n-1)}{4-3a_n}$$

$$a_{n+1}-\frac 13 = \frac{a_n-\frac 13}{4-3a_n}$$

So if no $a_n = \frac 13$ you have

$$\frac{a_{n+1}-1}{a_{n+1}-\frac 13} = 3 \frac{a_n-1}{a_n-\frac 13} = 3^n \frac{a_1-1}{a_1-\frac 13}$$

Of course you need to take care of the case where $a_1=\frac 13$.

Answer 3

Define the function $$ f(a)=\frac1{4-3a}\tag1 $$ Note that $$ \begin{align} f(a)-a &=\frac{(3a-1)(a-1)}{4-3a}\tag{2a}\\ &\left\{\begin{array}{} \lt0&\text{if }a\in\left(\frac13,1\right)\cup\left(\frac43,\infty\right)\\ \gt0&\text{if }a\in\left(-\infty,\frac13\right)\cup\left(1,\frac43\right) \end{array}\tag{2b} \right. \end{align} $$ Consider the two sequences for $n\in\mathbb{Z}$, $$ \begin{align} p_n &=\frac{3^{n-1}+1}{3^n+1}\tag{3a}\\ &=\frac13\left(1+\frac2{3^n+1}\right)\tag{3b} \end{align} $$ and $$ \begin{align} q_n &=\frac{3^{n-1}-1}{3^n-1}\tag{4a}\\ &=\frac13\left(1-\frac2{3^n-1}\right)\tag{4b} \end{align} $$ where $q_0=\pm\infty$.

Note that $$ \begin{align} f(p_n)&=p_{n+1}\tag{5a}\\ f(q_n)&=q_{n+1}\tag{5b} \end{align} $$ where, in the case of $q_0$, $$ \begin{align} f(q_{-1})&=f\!\left(\tfrac43\right)=\infty=q_0\tag{6a}\\ f(q_0)&=f(\infty)=0=q_1\tag{6b} \end{align} $$ Define the intervals $$ \begin{align} P_n&=(p_{n+1},p_n)\tag{7a}\\ Q_n&=(q_n,q_{n+1})\tag{7b} \end{align} $$ where $Q_{-1}=\left(\frac43,\infty\right)$ and $Q_0=\left(-\infty,0\right)$:

In the animation above, the solid red and green lines are the $P_n$ and $Q_n$. The arrows point to the dotted intervals $P_{n+1}$ and $Q_{n+1}$. The intervals are red if $f(a)\lt a$ on that interval and green if $f(a)\gt a$; these intervals are described in $(2)$.

Since $f'(a)\gt0$ except at $q_{-1}=\frac43$ (which is between $Q_{-2 }$ and $Q_{-1}$), we have the bijections $$ \begin{align} f&:P_n\to P_{n+1}\tag{8a}\\ f&:Q_n\to Q_{n+1}\tag{8b} \end{align} $$ Since $$ \bigcup_{n\in\mathbb{Z}}P_n\cup\bigcup_{n\in\mathbb{Z}}Q_n\cup\left\{p_n:n\in\mathbb{Z}\right\}\cup\left\{q_n:n\in\mathbb{Z}^{\ne0}\right\}=\mathbb{R}\tag9 $$ $(5)$ and $(8)$ show that for all points except $\left\{q_n:n\le0\right\}\cup\{1\}$, iterating $f$ will produce a seqence converging to $\frac13$ (one might even say that $q_{-\infty}=1$).

Answer 4

Hint: If $a_1<1$, it is easy to see $a_n<1$ and then let $b_n=a_n-\frac13$. If $a_1\in(1,\frac43)$, it is easy to see $a_n\in(1,\frac43)$ and then let $b_n=a_n-1$. You can do the rest.

Answer 5

Without induction.

If you follow the steps described here which I used answering this question making the story short $$a_{n+1}=\frac{1}{4-3 a_{n}} \qquad \text{with} \qquad a_1=c$$ $$a_n=\frac 13\frac{c \left(3^n-9\right)-(3^n-3) } {c(3^n-3)-(3^n-1) }$$

Now, you need to consider the various cases to arrive to the nice results from @Brian M. Scott's nice analysis.