4

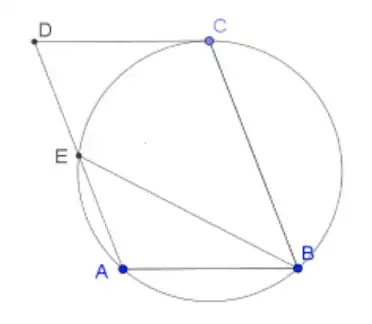
As shown in the diagram, $ABCD$ is a parallelogram where $DC$ is tangent to the circumcircle of $\triangle ABC$ which intersects $AD$ at $E.$ If $AB = 4$ and $BE = 5,$ find the length of $DE.$

enter image description here

Firstly, I noted that Power of Point could be used in this problem. I let $DE = x$ and I setup the equation $$x \cdot (x+AE) = 16,$$ since $AB = CD.$ However, from here, I got stuck as I do not know how to use the fact that $BE = 5.$ Can somebody help me?

Parcly Taxel
  • 105,904
questionasker
  • 1,171
  • 6
  • 20

2 Answers2

4

Since $AE$ and $BC$ are parallel, $ABCE$ is a symmetric trapezium, implying $CE=4$ and $AC=5$. By Ptolemy's theorem $$(x+AE)AE+4^2=5^2\implies (x+AE)AE=9$$ With the equation you already have, this produces the result $x=16/5$ and $AE=9/5$.

Parcly Taxel
  • 105,904
3

Note $\angle DAB = \angle DCB$, which means the arcs $EB$ and $CB$ are equal due to the shared arc $EC$. Then, $EB = CB= DA$ and, per the power of point $$DE=\frac{DC^2}{DA} = \frac{AB^2}{EB} = \frac{16}5$$

Quanto
  • 120,125