0

My question comes from here: Lax-Wendroff method for linear advection - Stability analysis, but nobody needs to know anything about Lax-Wendroff. My question is very easy.

Basically, in the last line of the answer, it is claimed that

$$|1+4(x^4-x^2)|\leq 1$$ is satisfied if $|x|\leq1$.

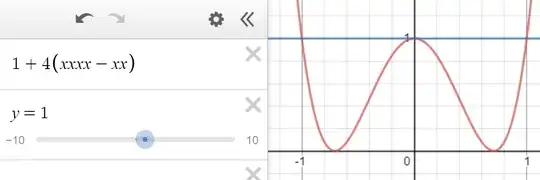
And I drew a plot to confirm this: enter image description here

My question is, how do I obtain the desired inequality $|x|\leq1$ algebraically?

José Carlos Santos
  • 440,053
Hyewon
  • 369
  • The question in the title is the converse of the question in the body of the question. Do you want to show that that inequality implies $|x|\le1$ or the other way around??? – David C. Ullrich Dec 11 '20 at 14:13
  • I guess a sufficient condition is what we want for stability, but I wanted to know if we could get the final inequality to be as big as possible, so I wanted what I asked (if you get what I mean) – Hyewon Dec 11 '20 at 14:20
  • If I got what you meant I wouldn't be asking. There are two different questions above - which one is the one you meant to ask????? – David C. Ullrich Dec 11 '20 at 14:21
  • Sorry for not being clear; I wanted to show that the inequality implies $|x|\leq 1$ – Hyewon Dec 11 '20 at 14:22

3 Answers3

4

Note $|(2x^2-1)^2|\le1$ iff $-1\le2x^2-1\le1$, i.e. $0\le x^2\le1$.

J.G.
  • 118,053
3

Assume that $|x| > 1$, now we have $x^4 > x^2$, so $|1+\text{something positive}| > 1$ always. Hence, the opposite.

David C. Ullrich
  • 92,839
V.G
  • 4,262
1

You can do it as follows:\begin{align}\bigl|1+4(x^4-x^2)\bigr|\leqslant1&\iff\bigl(1+4(x^4-x^2)\bigr)^2\leqslant1\\&\iff8(x^4-x^2)+16(x^4-x^2)^2\leqslant0\\&\iff(x^4-x^2)\bigl(1+2(x^2-x^2)\bigr)\leqslant0\\&\iff(x^4-x^2)\bigl(x^4+(x^2-1)^2\bigr)\leqslant0\\&\iff x^2(x^2-1)\leqslant0\\&\iff x^2\leqslant1\\&\iff x\in[-1,1].\end{align}

José Carlos Santos
  • 440,053