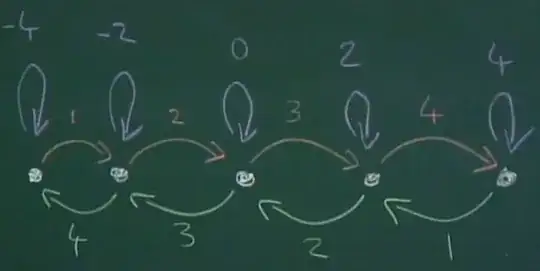3

${\frak sl}(2)= \left\{ \begin{bmatrix}a & b \\ c & d \end{bmatrix}: a + d=0\right\}= \text{span}\left\{H,E,F\right\}$

where $H = \begin{bmatrix}1 & 0 \\ 0 & -1 \end{bmatrix},$ $E = \begin{bmatrix}0 & 1 \\ 0 & 0 \end{bmatrix}$ and $F = \begin{bmatrix}0 & 0 \\ 1 & 0 \end{bmatrix}.$

Also, the brackets $[H,E]=2E,$ $[H,F]=-2F$ and $[E,F]=H$ provide an alternative (isomorphic) way of understanding the Lie algebra. With some handwringing after the last sentence it seem clear, but then the pictorial creativity is unleashed at the beginning of this nice lecture with this representation of the $5$-dimensional representation:

enter image description here

The dots represent "basis elements" and $E$ (in orange) sends each element to the next one from left to right, while $F$ (green) does the opposite, and $H$ in purple sends each element to itself. The numbers denote multiplicity.

The lecturer at that point picks the fourth white dot from the left calling it a vector, and he checks the basic arithmetic following the arrows and multiplicity notations to confirm that $[E,F]=H$ as $EF - FE=6 - 4= 2.$

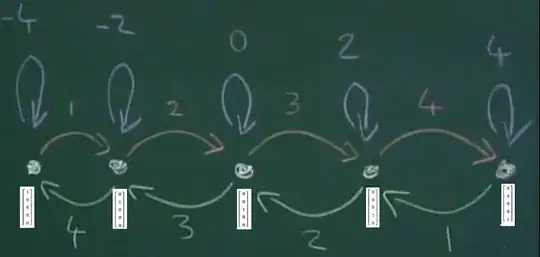
Very elegant, but can you please show me what that vector ("basis elements") - the white dots - would look like so that I can reproduce what's being done with basic linear algebra matrix to vector multiplication?

As it turns out, a lot of meaningful information as it pertains to the actual issue behind the question is buried in comments, so here is a summary. Besides the matrices provided in the accepted answer, there is a different set that matches - up to some possible sign adjustment of doubtful conceptual relevance - the diagram (thank you @Torsten Schoeneberg) as such:

enter image description here

$$\begin{align} H&=\Tiny{\begin{bmatrix}\color{blue}4&0&0&0&0\\0&\color{blue}2&0&0&0\\0&0&\color{blue}0&0&0\\0&0&0&\color{blue}{-2}&0\\0&0&0&0&\color{blue}{-4}\end{bmatrix}}\\ E&=\Tiny{\begin{bmatrix}0&\color{orange}4&0&0&0\\0&0&\color{orange}3&0&0\\0&0&0&\color{orange}2&0\\0&0&0&0&\color{orange}1\\0&0&0&0&0\end{bmatrix}}\\ F&=\Tiny{ \begin{bmatrix}0&0&0&0&0\\\color{green}{1}&0&0&0&0\\0&\color{green}{2}&0&0&0\\0&0&\color{green}{3}&0&0\\0&0&0&\color{green}{4}&0\end{bmatrix}} \end{align} $$

These matrices do fulfill the bracket relationships, and follow the diagram to a sign change, reflecting the multiplicity values written in colors on the board. For example $e_4=\Tiny\begin{bmatrix}0&0&0&1&0\end{bmatrix}^\top,$ corresponding to the fourth white dot, and performing the bracket $[E,F]:$ This is the composition $E\circ F(e_4)$. Starting with $EF,$ $F\cdot e_4=4 e_5$ and composing this result with $E,$ we obtain $4 e_4.$ Whereas $FE$ will entail starting with $E\cdot e_4 = 2 e_3$ which then becomes $2F\cdot e_3=6e_4.$ Therefore $4e_4-6e_4=-2e_4,$ as opposed to the positive $2$ in the lecture.

The leftward extreme example $\Tiny e_1=\begin{bmatrix}1&0&0&0&0\end{bmatrix}^\top,$ under the action of the same bracket should result in $4e_1-\mathbf 0=4e_1.$ Following the diagram, $EF$ would turn out $0,$ because there is no green arrow originating in the first dot, and $FE$ would be $4e_1,$ which would pick up a $-$ in the commutator.

Antoni Parellada
  • 10,239
  • 2
    The Lie algebra you wrote is $\mathfrak{sl}(2)$, not $\mathfrak{su}(2)$. Regardless, the $n$-dimensional representation $V_n$ is just $S^n V_2$, the n-th symmetric power of the (defining) 2-dimensional representation. If you let $x,y$ be a basis for $V_2$, then a basis for $V_{n+1}$ is $x^n, x^{n-1} y, \dots , y^n$ and you can check by hand that e.g. $H$ acts by $-n, 2-n, \dots , n-2, n$ etc. – Sebastian Schulz Dec 10 '20 at 18:00
  • @SebastianSchulz Thank you. Yes, sloppy mistake edited now. What would $x$ and $y$ would look like in your comment? – Antoni Parellada Dec 10 '20 at 18:06
  • 1
    Hey, I've been thinking about this again. So are you saying that if the purple row at the top of the board were $4 , 2 , 0 , -2 , -4$ instead of $-4, -2, 0, 2, 4$, everything would make sense? If that's the case, I wonder if it's maybe really just a glitch by the lecturer. – Torsten Schoeneberg Jul 08 '21 at 21:24

1 Answers1

2

Consider these three $5\times5$ matrices:$$\mathcal H=\begin{bmatrix}4&0&0&0&0\\0&2&0&0&0\\0&0&0&0&0\\0&0&0&-2&0\\0&0&0&0&-4\end{bmatrix},\ \mathcal E=\begin{bmatrix}0&4&0&0&0\\0&0&6&0&0\\0&0&0&6&0\\0&0&0&0&4\\0&0&0&0&0\end{bmatrix}\text{, and }\mathcal F=\begin{bmatrix}0&0&0&0&0\\1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\end{bmatrix}.$$If $aE+bF+cH\in\mathfrak{sl}_2$, consider the matrix $a\mathcal E+b\mathcal F+c\mathcal H$. It's a $5\times5$ matrix and this defines a $5$-dimensional representation of $\mathfrak{sl}_2$ since, as you can check, $[\mathcal H,\mathcal E]=2\mathcal E$, $[\mathcal H,\mathcal F]=-2\mathcal F$, and $[\mathcal E,\mathcal F]=\mathcal H$.

José Carlos Santos
  • 440,053
  • 1
    No; the white dots are the elements of the standard basis of $\Bbb C^5$. Take, for instance $e_1=(1,0,0,0,0)$. Then the action of $H$ on $e_1$ is given by $\mathcal H.e_1=(4,0,0,0,0)=4e_1$. – José Carlos Santos Dec 10 '20 at 18:31
  • 1
    In my answer to https://math.stackexchange.com/q/3318978/96384, I used Bourbaki's normalisation of the basis vectors which here ($n=5$) literally gives (Jose's $H$ and) $E=\begin{bmatrix}0&4&0&0&0\0&0&3&0&0\0&0&0&2&0\0&0&0&0&1\0&0&0&0&0\end{bmatrix}$ and $F=\begin{bmatrix}0&0&0&0&0\-1&0&0&0&0\0&-2&0&0&0\0&0&-3&0&0\0&0&0&-4&0\end{bmatrix}$, and again the "dots" are literally just the standard basis vectors $e_i$ of $\mathbb C^5$. After a base change $e_2 \mapsto -e_2$, $e_4 \mapsto -e_4$, one gets rid of the minus signs and thus exactly what is described in the diagram in the OP. – Torsten Schoeneberg Dec 10 '20 at 22:43
  • @TorstenSchoeneberg I am completely unfamiliar with what we are doing here, so I wonder if you could bear with me on this one. The base change is particularly confusing... Say you want to replicate exactly what is in the OP, i.e. [EF - FE] applied to the fourth white dot. Presumably, the fourth white dot is $\begin{bmatrix}0,0,0,1,0\end{bmatrix}^\top,$ which after the base change ends up being $\begin{bmatrix}0,0,0,-1,0\end{bmatrix}^\top.$ – Antoni Parellada Dec 11 '20 at 03:05
  • The operation $F\cdot (-e_4)$ results in $4e_5.$ Now performing $E\cdot 4e_5=E\begin{bmatrix}0,0,0,0,4\end{bmatrix}^\top$ yields $4 e_4= \begin{bmatrix}0,0,0,4,0\end{bmatrix}^\top.$ Likewise, performing first $E\cdot(-e_4)=-2e_3= \begin{bmatrix}0,0,-2,0,0\end{bmatrix}^\top,$ and later $F$ acting on the result yields $6 e_4 = \begin{bmatrix}0,0,0,6,0\end{bmatrix}^\top.$ The bracket would be $-2e_4 = \begin{bmatrix}0,0,0,-2,0\end{bmatrix}^\top,$ but it doesn't make sense. – Antoni Parellada Dec 11 '20 at 03:13
  • Ah you're right, the last base change I wrote there actually is bad, it would introduce minus signs in the matrix for $E$. I would love to expand all that, unfortunately I am quite constrained on time for the next couple of days. – Torsten Schoeneberg Dec 11 '20 at 03:55
  • Haha, it boils down to the fact that your $F$ is my $\color{red}{-}y$ in the linked post. So in fact just scrap the minusses in the matrix for $F$ in my first comment and everything I wrote about base change. Then the calculations you tried there should work. Sorry. – Torsten Schoeneberg Dec 11 '20 at 04:04
  • @TorstenSchoeneberg it still results in $-2e_4$ when I change the signs for $F$ without the base change. – Antoni Parellada Dec 11 '20 at 04:34
  • 1
    Right, there's something wrong with the order too. Ignore everything I wrote. No worries, I will get back to that, it will not let me sleep. Gnarf. – Torsten Schoeneberg Dec 11 '20 at 05:03