$x^3 + y^3 = p^2$ has a solution over the integers for some three digit prime p. Find all p that satisfy.
The first thing I did was factorize the left hand side, getting $(x+y)(x^2 - xy + y^2) = p^2$
I then considered the case $x^2 - xy + y^2 = p^2$, which gave me $p^2 = 3y^2 -3y +1$, which can be naturally factorized into $(p+1)(p-1) = 3y(y-1)$, but how do I do anything with this? I don't see a continuation from this point onwards.
Any hints or solutions would be greatly appreciated. Thanks!
Consider the linear factor first instead; this allows you to directly express $y$ in terms of $x$. From $$p^2=x^3+y^3=(x+y)(x^2-xy+y^2),$$ it follows that $x+y=p^k$ for some $k\in\{0,1,2\}$, and $x^2-xy+y^2=p^{2-k}$. Then $y=p^k-x$, so we can eliminate $y$ to get the quadratic equation $$3x^2-3p^kx+p^{2k}-p^{2-k}=0.$$ A quadratic has an integral root if and only if its discriminant is a perfect square. Can you continue from here?
The discriminant equals $$\Delta=(-3p^k)^2-4\cdot3\cdot(p^{2k}-p^{2-k})=-3p^{2k}+12p^{2-k}.$$ For $k=1$ and $k=2$ this becomes $$\Delta=-3p^2+12p=-3p(p-4)\qquad\text{ and }\qquad\Delta=-3p^4+12,$$ which are both negative because $p>4$. Hence $k=0$ and $\Delta=12p^2-3$. So if $p$ is such a prime, then $\Delta$ is a perfect square and a multiple of $3$, say $\Delta=(3e)^2$. Then a bit of algebra shows that $(X,Y)=(2p,e)$ is an integral solution to the Pell equation $$X^2-3Y^2=1.$$
Take $u = 6y-3.$ The first few values of $p$ in $u^2 - 12 p^2 = -3$ are $$ 1, 13, 181, 2521, 35113, ... $$ subject to $$ p_{j+2} = 14 p_{j+1} - p_j $$
and $p=181$ is a three digit prime
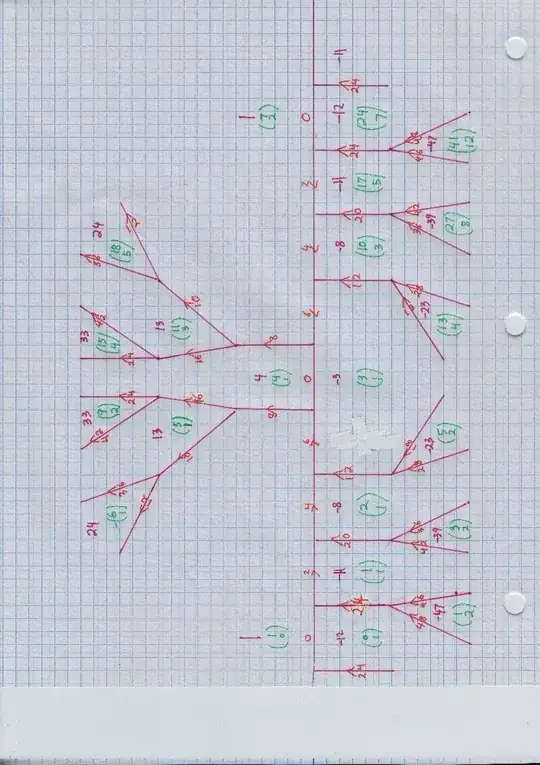
Here is a portion of the Conway Topograph for $u^2 - 12 p^2.$ A continuation a little bit in the direction of increasing $(u,p)$ would show the next occurrence of $u^2 - 12 p^2 = -3$ at $(45, 13).$ That recipe is $$ (u,p) \mapsto (7u+24p, 2u + 7p) $$ This is multiplication of a column vector by the square matrix $$ \left( \begin{array}{cc} 7&24 \\ 2&7 \end{array} \right) $$ which has determinant $1$ and trace $14.$ It follows from Cayley-Hamilton for this matrix that
$$ u_{j+2} = 14 u_{j+1} - u_j $$
$$ p_{j+2} = 14 p_{j+1} - p_j $$ You can also work it out by hand from
$$ \left( \begin{array}{c} u_{j+1} \\ p_{j+1} \end{array} \right) = \left( \begin{array}{cc} 7&24 \\ 2&7 \end{array} \right) \left( \begin{array}{c} u_j \\ p_j \end{array} \right) $$ write out the values at $j+2$ and substitute some things
Here are the first few values of $p$ after $1.$ Some of them are prime.
13 = 13
181 = 181
2521 = 2521
35113 = 13 37 73
489061 = 489061
6811741 = 6811741
94875313 = 13 61 181 661
1321442641 = 1321442641
18405321661 = 18405321661
256353060613 = 13 757 2521 10333
3570537526921 = 277 3037 4244329
