Finding a function which is distance $1$ from $x^2$ along its normals

Question

So I recently thought of a problem, which I have tried to solve many ways but couldn't. It's very simple to describe...

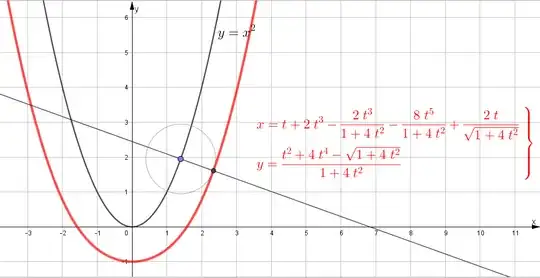
Find the function which is distance $1$ from parabola $y=x^2$ along its normals. Visual of what I mean.

---

This one of the things I've tried...

This function would get the corresponding $x$ value on the function we want to find from an $x$ value on curve $y=x^2$. The inverse would give the corresponding $x $ value on $x^2$ for a given $x$ value which would make it trivial to determine the $y$ value. $$ f(x)=x+\sin(\arctan(2x)) $$ This can be resolved to this... $$ f(x)=x+\frac{2x\sqrt{1+4x^2}}{1+4x^2} $$ However I don't know how to get the inverse of this function.

Answer 1

$(f-x)=2x/\sqrt{1+4x^2}$ so $(f-x)^2(1+4x^2)=4x^2$ or, according to Wolfy, $4 f^2 x^2 + f^2 - 8 f x^3 - 2 f x + 4 x^4 - 3 x^2 = 0$.

This is a quartic in $x$ which can be solved but is incredibly messy as expected.

Answer 2

I have found parametric equations of the locus

$$ \begin{cases} x=2 t^3-\frac{8 t^5}{4 t^2+1}-\frac{2 t^3}{4 t^2+1}+t +\frac{2 t}{\sqrt{4 t^2+1}}\\ y= \frac{4 t^4+t^2-\sqrt{4 t^2+1}}{4 t^2+1}\\ \end{cases} $$

---

Answer 3

We can modify by offsetting from standard parametrization. Used $ f=1, r= (-0.2,0,+0.2)$ in the plot ( used offset 0.2 in place of 1.0 for graph clarity ).

f = 1; r = 0;
g1 = ParametricPlot[{2 f t, f t^2} + 
   r {-t/Sqrt[1 + t^2], 1/Sqrt[1 + t^2]}, {t, -1, 1}, 
  GridLines -> Automatic]
 r = 0.2;
g2 = ParametricPlot[{2 f t, f t^2} + 
   r {-t/Sqrt[1 + t^2], 1/Sqrt[1 + t^2]}, {t, -1, 1}, 
  PlotStyle -> {Thick, Blue}]
r = -0.2;
g3 = ParametricPlot[{2 f t, f t^2} + 
   r {-t/Sqrt[1 + t^2], 1/Sqrt[1 + t^2]}, {t, -1, 1}, 
  GridLines -> Automatic, PlotStyle -> {Thick, Red}]
Show[{g1, g2, g3}, PlotRange -> All]

We add or remove distances along normal and the tangent with offset $r$ $$ (x,y)= ( 2 f t,f t^2 ) ;\; t = \tan \phi $$

$$ x_1= x - r \sin \phi, y_1= y+ r \cos \phi $$