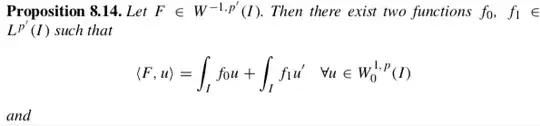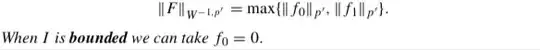Let $I$ be an interval and $W^{-1,p'}(I)$ be the dual space of $W^{1,p}_0(I)$ ($1\leq p<\infty$). Brezis says
My question is on
Remark 19. The functions $f_0$ and $f_1$ are not uniquely determined by $F$.
Is the following argument correct?
Here is my counterexample: let $I=(0,1)$. Let $g_{0}=f_{0}$ and $g_{1}=f_{1}+c$ for some constant $c\neq0$.
From $f_{1}\neq g_{1}$, it suffices to show $\int_{I}g_{1}v'=\int_{I}f_{1}v'$ for $H^1_0(I)$.
But from $c,v\in H^{1}(I)$ we have
$$\int_{I}cv'=cv(1)-cv(0)-\int_{I}0\times v,$$
but from $v\in H_{0}^{1}(I)$ we have $v(1)=0=v(0)$. Hence $$\int_{I}g_{1}v'=\int_{I}f_{1}v'+0.$$
Thus, we conclude $\langle F,v\rangle = \int_{I}g_{0}v+\int_{I}g_{1}v'$ with $g_1\neq f_1$.
One concern is that the above calculation implies we have $\int_{I}v'=0$ for $v\in H^1_0(I)$, which I never thought about (but now I think of e.g. the hat function, the integral of its derivative Heaviside function is indeed $0$).
Another concern is that an answer in characterization of the dual space of the Sobolev space $H_0^1$
contains a "quote" from Brezis Prop. 9.20, saying that "$(1)$: $ \, v^0,v^1,
\dots , v^n$ is NOT determined uniquely by $v\in H^{-1}$, that is, $v_0$ can be varied". Note that this (that $v_0$ can be varied) is not claimed in Brezis book.
Anyway, in my example above, $v_0$ is the same but it is $v_1$ that is different.