Closed set written as an union of images of curves implies that at least one of those images is closed?

Question

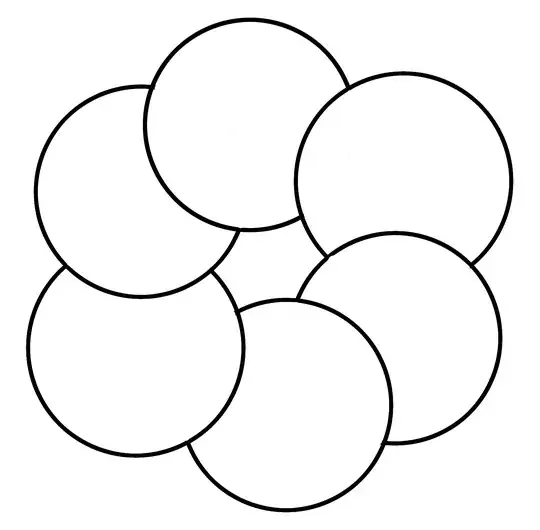
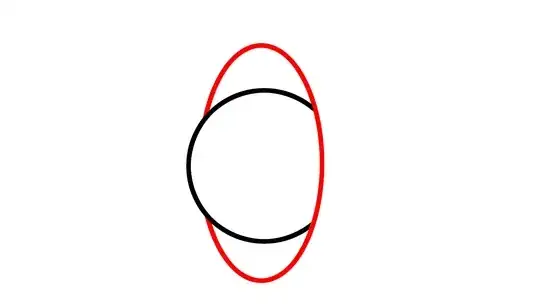
Let $A\in \mathbb{R}^2$ be a closed set. Suppose $A=\bigcup_{i\in\Lambda}U_i$ as a disjoint union, where $U_i$ is the image of some $C^1$ injective curve $\gamma_i:\mathbb{R}\to\mathbb{R}^2$. There is $j\in\Lambda$ such that $U_j$ is closed?

I suspect you forgot the adjective "injective" for $\gamma_i$'s. — Moishe Kohan, Nov 27 '20 at 15:17
Related: https://math.stackexchange.com/questions/1907925/can-one-partition-the-plane-mathbbr2-by-closed-intervals-of-equal-length/1909655#1909655 — Moishe Kohan, Nov 27 '20 at 15:27

Ruy · Accepted Answer · 2020-11-27T16:47:09.003

3

I am told to add at least 30 characters but isn't a picture worth a thousand words?

EDIT. Two curves are enough!

edited Nov 27 '20 at 16:47

answered Nov 27 '20 at 15:45

Ruy

20,073

Beautiful! Thanks! – JPMarciano Nov 27 '20 at 15:54

Closed set written as an union of images of curves implies that at least one of those images is closed?

1 Answers1