8

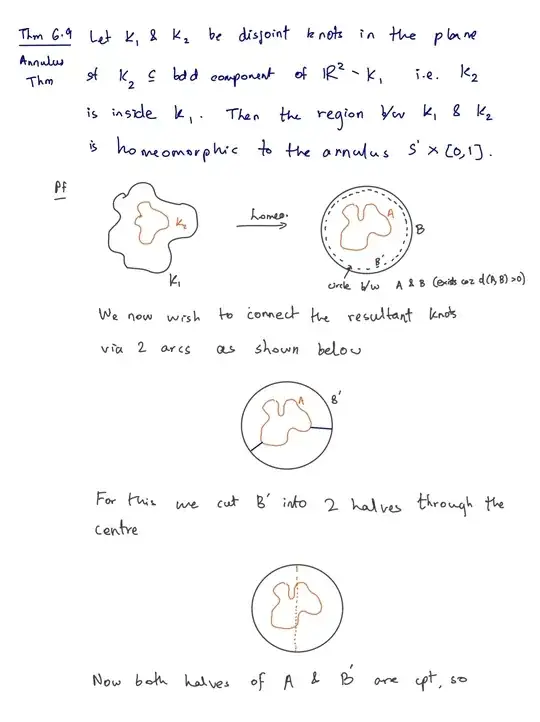
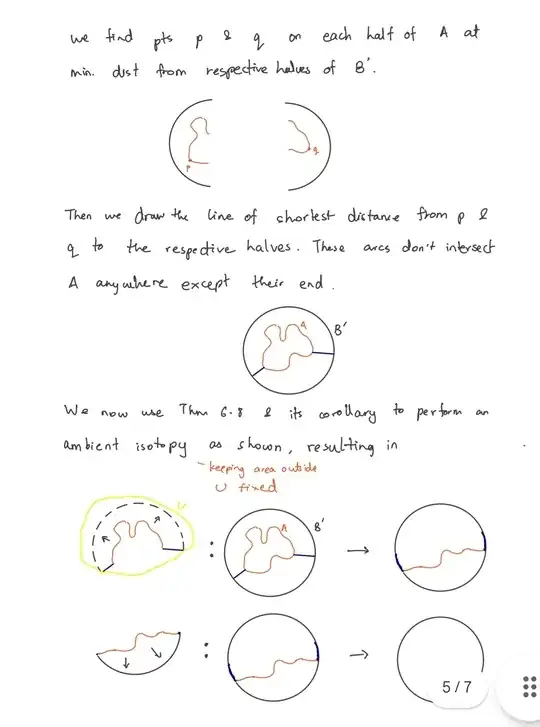
I'm trying to read Rolfsen's "Knots and Links" and I'm a little discouraged that I can't do one of the first and seemingly more important exercises. The question is

Use the Schoenflies theorem (every topological imbedding $S^1 \rightarrow \mathbb{R}^2$ is the boundary of a 2-disk) to prove the annulus theorem: Given two disjoint imbeddings of $S^1$ in $\mathbb{R}^2$, where one is "inside" the other (I.e. one is in the bounded component of the complement of the other), then the space "between" the two curves is homemorphic to $S^1 \times [0,1]$.

There is a hint that says "connect the two curves with arcs". Unfortunately I can't say much about "what I've tried." At this point in the book, we know only that all simple closed curves in $\mathbb{R}^2$ or $S^2$ are "equivalent" in the sense that there exists a homeomorphism of the ambient space taking one to the other. This allows us to assume one of the curves is the standardly imbedded $S^1$. After that I'm totally unsure of what to do. I would appreciate any hints or advice. Thank you for reading my question.

Mr. Cooperman
  • 6,231
  • Are you sure you weren't introduced to a stronger fact: if $A,B\subseteq {\bf R}^2$ are homeomorphic to $S^1$ and $f\colon A\to B$ is a homeomorphism, then there is a homeomorphism $\overline f\colon {\bf R}^2\to {\bf R}^2$ such that $f\subseteq \overline f$? – tomasz May 14 '13 at 01:16
  • Note that the statement is not true if $A,B$ are homeomorphic to pairs of circles (because of orientation issues), so there's no point trying something like that. – tomasz May 14 '13 at 01:20
  • Hi Tomasz. Yes I actually know that to be true. Is the desired result a more-or-less immediate consequence? If so Ill think about your hint for a while. Also I like your notation for restriction :) – Mr. Cooperman May 14 '13 at 01:21
  • I'm not sure, but I recall those two result being in proximity during the Euclidean topology course I had taken last year. Right now I'm a little sleepy, so I won't help much more for now. :) – tomasz May 14 '13 at 01:22
  • No worries, thanks for your help! – Mr. Cooperman May 14 '13 at 01:23

2 Answers2

4

I haven't thought this through carefully, but just following the hint:

Choose a point $a$ on the outer circle and a point $b$ on the inner circle. Join $a$ and $b$ with an arc that doesn't cross the two circles. Now "thicken up" this arc very slightly (and thicken up each of $a$ and $b$ to a very short piece of circular arc on their respective circles) so that now we have to the two circles with a very thin rectangle sitting between them. (I think that making this "thickened" picture rigorous is probably part of what is involved in translating the hint into a full argument.)

Now the consider the boundary of the union of the two circles and this rectangle. If you are picturing what I want you to picture, you will see that it is a circle. (Just to be sure: if you take an annulus and snip out a small rectangle joining the inner and outer annulus, you get a kind of "sliced" annulus which is homeomorphic to a disk with circle as boundary. But you can verify that the boundary of the region I am describing is a circle without knowing that the region between the two circles is an annulus just follow the outer circle around from the top left corner of the rectangle all the way around to the top right corner, then move along the right boundary of the rectangle to its bottom right corner, now go back around the inner circle to the bottom left corner of the rectangle, and now go back up the left edge of the rectangle to get back where you started: you've described a circle.) So it bounds a disk. So the region between the two circles, with a thin rectangle removed, is a disk. Gluing back in the rectangle should make into an annulus, as required.

user302934
  • 1,738
  • 1
  • 9
  • 27
Matt E
  • 127,227
  • Thanks, Matt. The only part I'm unsure about is the tubular neighborhood you're talking about. Do such things exist in the topological setting? I understand I can make the arc smooth, but the points where it meets the curves may look very bizarre. – Mr. Cooperman May 14 '13 at 02:00
  • oh I think I see what you're saying. There's no need to actually take a tubular neighborhood. all you need is two disjoint arcs that cut the "in between" region into two disks that intersect at the arcs! – Mr. Cooperman May 14 '13 at 02:12
  • @Tim: Dear Tim, That's right. I'm not sure about filling in all the details. I think it must be possible, given that the hint seems to be pushing very strongly in this direction, but I'm a little shaky in filling details in this kind of pure topology! Best wishes, – Matt E May 14 '13 at 02:26
  • I don't understand your proof, why should you get an annulus on gluing back the rectangle? Also I'm not sure you can always draw such a rectangle so that it doesn't intersect the two embeddings. – Anay Jain Aug 29 '24 at 16:27
1

Theorem 6.9 in the below pictures should answer your question. I proved it with my classmate Sanchit Nayak while doing Rolfsen's book. enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

Anay Jain
  • 300
  • 1
  • 10
  • Use Mathjax to write math instead of posting images. – Moishe Kohan Dec 08 '24 at 19:32
  • 1
    @MoisheKohan I had to include the knot diagrams anyway, so just saving myself some work – Anay Jain Dec 11 '24 at 14:08
  • This is not how this site works. – Moishe Kohan Dec 11 '24 at 14:22
  • How are we to present topological proofs which are so heavily visual? – Anay Jain Dec 12 '24 at 04:04
  • You have read some topology textbooks, right? Then you know how it is done. In Mathstackexchange, you write text using Mathjax (for professional math papers it would be latex) and add pictures for illustration. – Moishe Kohan Dec 12 '24 at 04:12
  • @MoisheKohan I only wrote this answer because I found no decent proof for it on this site. If you wish I painstakingly typset the text and paste the images in the right order, I know it will take me more time than I am willing to give an answer I have already written down neatly in detail. If you find this presentation troublesome would you rather not have this answer here? If the majority shares your opinion, and this answer receives more downvotes then upvotes, I will delete it. – Anay Jain Dec 12 '24 at 04:27