2

I encountered a question from Khan Acad that asked, at what intervals of x does the function increase. My intuition is that all ranges except for 0 and 1, because tangents at those points are flat per green graph below. Backed up by the red graph, showing h'(1)=0 & h'(0)=0, zero velocity.

I need help figuring out my knowledge gap:

  • Am I misinterpreting what "increasing" here?
  • Am I missing the point of what a critical point is..?

enter image description here

enter image description here

nvs0000
  • 681

2 Answers2

4

Increasing functions and strictly increasing functions are both well-defined terms with different definitions.

From wikipedia:

In calculus, a function $f$ defined on a subset of the real numbers with real values is called monotonic if and only if it is either entirely non-increasing, or entirely non-decreasing. That is, a function that increases monotonically does not exclusively have to increase, it simply must not decrease.

A function is called monotonically increasing (also increasing or non-decreasing), if for all $x$ and $y$ such that $x\leq y$ one has $f(x)\leq f(y),$ so $f$ preserves the order. Likewise, a function is called monotonically decreasing (also decreasing or non-increasing) if, whenever $x\leq y$, then $f(x)\geq f(y)$, so it reverses the order.

If the order $\leq$ in the definition of monotonicity is replaced by the strict order $<$, then one obtains a stronger requirement. A function with this property is called strictly increasing. Again, by inverting the order symbol, one finds a corresponding concept called strictly decreasing. A function may be called strictly monotone if it is either strictly increasing or strictly decreasing. Functions that are strictly monotone are one-to-one (because for $x$ not equal to $y$, either $x<y$ or $x>y$ and so, by monotonicity, either $f(x) <$ $f(y)$ or $f(x) > f(y)$ (thus $f(x) \neq f(y)$.)

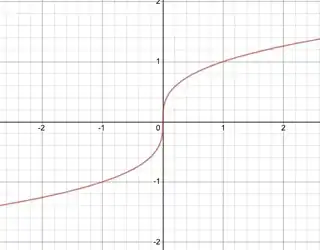
As B.Martin pointed out in the comments, $f(x)=x^3$ is a strictly increasing function (!), with $f′(0)=0$. Also, the constant function $f(x)=1$ is an increasing (but not strictly increasing) function with a derivative that is $0$ everywhere. So one always has to be clear what one is talking/asking about: whether or not a function is increasing or strictly increasing? At a point in the domain, or a subset of the domain, or over the entire domain?

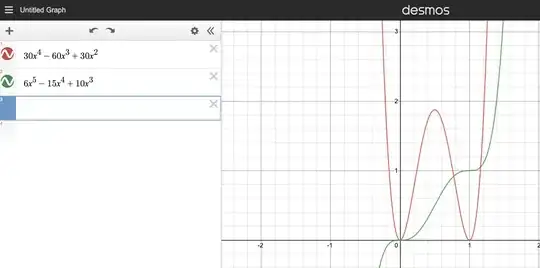
Your/Khan academy's question is: Is the function $f(x) = 6x^5 - 15x^4 + 10x^3$ increasing (but not necessarily strictly increasing) for all $x \in \mathbb{R}$?

The answer is yes. In fact, your function is strictly increasing for all $x \in \mathbb{R}$, exactly the same as how $f(x) = x^3$ is strictly increasing for all $x \in \mathbb{R}$.

We may also talk about a function being strictly increasing at a point. See: https://math.stackexchange.com/a/364619/29156 for details. (Although, Did's definition of increasing at a point is really a definition of "strictly increasing at a point", since we are going with wikipedia's definitions). The domain $D$ of all points for which $f(x)$ is increasing is the set $D = $ { $x: f(x)$ is increasing at the point $x$ }.

The function $f(x) = 6x^5 - 15x^4 + 10x^3$ is in fact strictly increasing at the point $x=0$, and it's also true that $f'(0)=0$. However, we only need to show that this function is increasing, and we can prove this using the definition of "increasing", or we can use the fact that $f'(x) \geq 0$ $\forall x \in \mathbb{R}$, which can be seen from the graph, or by noting that $f'(x) = (\sqrt{30}x(x-1))^2 \geq 0 \ \forall x \in \mathbb{R}$.

Going back to your question, "... because tangents at those points are flat..."

What is your definition of "flat"?

Useful:

A (differentiable) function $f$ is increasing but not strictly increasing at a point $x=c$, i.e. $f'(c) = 0$, $\iff \exists \epsilon > 0 $ such that $f$ is constant on the interval $ (c - \epsilon, c + \epsilon)$. I think this fact also works for all functions, not just differentiable or continuous ones.

Adam Rubinson
  • 24,300
  • Thanks for this, so what you are saying, is that there are two definitions of "increasing". If we are looking for "increasing" in h(x) we can include points whose derivatives are zero. But if we are looking for "strictly increasing", we could not include derivatives whose points are zero? -//- What I meant by "flat": the derivative at points 1 and 0 are zero. (Ie. h'(1) = 0 & h'(0) = 0). – nvs0000 Nov 15 '20 at 05:08
  • 1
    Not quite. “But if we are looking for “strictly increasing”, we could not include points whose derivatives are zero”. Like I say, that’s not true. A function with finitely many points having derivative zero may be strictly increasing, like $f(x)=x^3$ or your function $f(x)=6x^5-15x^4+10x^3$. And I would avoid using the term, “flat”, the way you are using it. I’ve seen people use “flat” to mean undulation point, or a “flat function”, both if which are something more specific. I would avoid using the term altogether. Use “critical point”, or better, “stationary point”. – Adam Rubinson Nov 15 '20 at 11:03
  • So you are right that an increasing function can have stationary points. But like I said in my answer, a strictly increasing function can also have stationary points. Read carefully the definition of “strictly increasing” in my answer, and tell me why you think $f(x)= x^3$ is not strictly increasing. Just in case you can’t work it out from my answer (it’s not obviously unambiguous), Definition of strictly increasing is: If $ x < y$ then $f(x) < f(y)$. – Adam Rubinson Nov 15 '20 at 11:21
  • //[Point 1] To confirm, stationary means f'(x) = 0? //[Point 2] Sounds like my definition of "strictly increasing" isn't great. What I don't understand is the Wikipedia statement 'Functions that are strictly monotone are one-to-one (because for not equal to , either < or > and so, by monotonicity, either ()< () or ()>() (thus ()≠().)' Your explanation "Definition of strictly increasing is: If < then ()<()" while much better, I also don't get. Is there a concrete example, video, or graph that shows x<y and is strictly increasing? – nvs0000 Nov 15 '20 at 14:57
  • //[Point 3] is @tobymak's comment to me inaccurate then? – nvs0000 Nov 15 '20 at 14:57
  • Yes, a stationary point is one in which $f'(x)=0$. For a proof that $y=x^3$ is increasing, see: https://math.stackexchange.com/questions/758158/how-to-prove-x3-is-strictly-increasing/3908601#3908601 . In particular, I just posted a new answer to that question. Here is a video that might help to distinguish increasing functions from strictly increasing functions: https://www.youtube.com/watch?v=1mW6pOq7CsI Yes, I believe tobymak's confirmation of your comment is inaccurate because a strictly increasing function can have stationary points - points whose derivatives are zero - e.g. $y = x^3$. – Adam Rubinson Nov 15 '20 at 16:43
  • For the function $f(x)=x^3$, yes the derivative of $f(x)$ at $0$ is $0$. But this does not tell you whether or not the graph is strictly increasing at the point $0$. As $x$ approaches $0$ from below, $x^3 < 0$. And as $x$ approaches $0$ from above, $x^3>0.$ So the graph is increasing at the point $0$. – Adam Rubinson Nov 15 '20 at 16:53
3

A function $f$ is increasing if $f(b) ≥ f(a)$ with $b ≥ a$, for all $a,b$ in the domain, which is $x \in \mathbb R$ in your case. Note the $≥$ sign instead of $>$.

What you are thinking of is a strictly increasing function, otherwise called a monotonically increasing function. These functions can have (* see edit) $f'(x) = 0$, whereas an increasing function can $f'(x) = 0$ for a finite number of $x$ values.

Note that the derivative does not need to be defined at all points for a function to be an increasing function. For example, the function $g(x) = x^{1/3}$ increases for all $x \in \mathbb R$, despite the derivative not being defined at $x = 0$:

enter image description here

It is also possible for a function to be increasing in a restricted domain such as $(a,b)$, with other variations depending on whether the interval is open or closed.

Edit: Strictly increasing functions can have $f'(x) = 0$, as long as $f(x)$ is increasing in the neighbourhood of that point, say $(x - \epsilon, x + \epsilon)$ as mentioned by Adam Rubinson.

Toby Mak
  • 17,073
  • 1
    Shouldn't it say, "A function $f$ is increasing if $f(b) ≥ f(a)$ for all $a,b$ with $a\leq b$ in the domain" – Adam Rubinson Nov 14 '20 at 12:08
  • Thanks for the correction, my bad ;) – Toby Mak Nov 14 '20 at 12:09
  • 4
    $f(x) = x^3$ is a strictly increasing function, with $f'(0) = 0$, and $f(x) = 1$ is an increasing function with a derivative that is 0 everywhere. – Ben Martin Nov 14 '20 at 12:14
  • Thanks for this, so what you are saying, is that there are two definitions of "increasing". If we are looking for "increasing" in h(x) we can include points whose derivatives are zero. But if we are looking for "strictly increasing", we could not include derivatives whose points are zero? -//- What I meant by "flat": the derivative at points 1 and 0 are zero. (Ie. h'(1) = 0 & h'(0) = 0). – nvs0000 Nov 15 '20 at 05:09
  • Yes, that's correct. – Toby Mak Nov 15 '20 at 05:14
  • I have now edited my post to reflect what Adam Rubinson has said. – Toby Mak Nov 22 '20 at 11:45