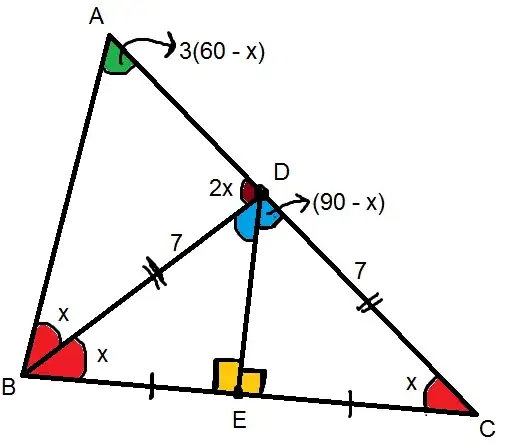
In $\Delta ABC,$ side $AC$ and the perpendicular bisector of $BC$ meet at $D$, where $BD$ bisects $\angle ABC$. If $CD = 7$ and $[\Delta ABD] = a\sqrt{5}$ , find $a$ .
What I Tried: Here is a picture:-
Let the perpendicular bisector of $BC$ pass through $BC$ at $E$ .
Then I first noticed that $\Delta BDE \cong \Delta CDE$ from $(SAS)$ congruency.
This gives the required information in the diagram, as well as we have $BD = 7$ .
Now :- $$\Delta ABD \sim \Delta ACB$$
$$\rightarrow \frac{AD}{AB} = \frac{7}{BC} = \frac{AB}{AC}$$
So let $AD = k$ , $AB = m$ , $BE = EC = n$ . We have :-
$$\frac{k}{m} = \frac{7}{2n} = \frac{m}{(7+k)}$$