Defining projection maps in Affine geometry and Thales' theorem and related sources

Question

I am from Physics background and have not much experience in dealing with rigorous mathematical language and proofs. Out of interest, I am trying to read the book Spacetime. The book, which seems advanced, is very hard for me to read due to my inexperience and lack of the coverage of its prerequisites. Here's an excerpt from the book on proving Thales' theorem,

As you can see, the author uses projection maps $\pi$ and $\vec{\pi}$ but no definitions of these maps have been given. The author assumes the reader is familiar with these definitions/concepts. And I am lost. Can someone kindly explain how these maps are defined (both rigorous and intuitive) and what are their properties, that are crucial for this proof?

Moreover, if you think I should consult other resources on affine and Euclidean geometry first before venturing into this book, kindly recommend those sources. (Please do not recommend Berger or Audin. Those seem even more difficult than this book)

Edit:

As I realized that, people are unlikely to have a copy of this book, I have decided to to add images of the first five pages of the book so that people can understand better the level of this book and that would help recommending resources.

Answer 1

An answer to the unedited version of the question.

I think in order to understand the quoted fragment of a proof is required basic knowledge on vector and affine spaces and their subspaces and quotient spaces. I expect it is sufficient to read Wikipedia articles devoted to these subjects. Concerning affine spaces, you can also start from my recent answer to the question “What is the affine space and what is it for?” and possible other stuff from that thread.

In the proof $\Bbb A^n$ should be the affine space associated to the vector space $\Bbb R^n$. Maps to equivalence classes usually are called quotient maps, not projections. The map $\pi$ is defined via the map $\vec\pi$, $\vec x$ is a coset $x+\vec H$, that is an set $\{x+y:y\in\vec H\}$, which is an element of $\Bbb R^n/\vec H$.

As I understood the context, by a hypersuface in the book is meant a hyperplane, that is a set $\{y\in\Bbb R^n: (y,x)=c\}$, where $x\in\Bbb R^n$ is a fixed non-zero vector, $c\in\Bbb R$ is a constant and $(\cdot,\cdot)$ is the inner product on $\Bbb R^n$.

Then the proof via quotient spaces looks overcomplicated. Indeed, since the hyperplanes $H_i$ are parallel, there exists a non-zero vector $x\in\Bbb R^n$ and constants $c_i\in\Bbb R$ such that $H_i=\{y\in\Bbb R^n: (y,x)=c_i\}$ for each $i$. Remark that we need a restriction $H_1\ne H_2$ missed in the lemma, because otherwise $x_2(l)-x_1(l)=0$. The the collinearity of points $x_i(l)$ implies that there exists $\lambda\in\Bbb R$ such that $x_3(l)-x_2(l)=\lambda(x_2(l)-x_1(l))$. Taking inner product with $x$ of both sides of this equality, we obtain that $c_3-c_2=\lambda (c_2-c_1)$, that is $$\frac{x_3(l)-x_2(l)}{ x_2(l)-x_1(l)}=\lambda=\frac {c_3-c_2}{c_2-c_1},$$which does not depend on $l$.

Update. I read the first paragraph of the first page of the book and briefly looked at the next pages and I guess that the affine space $\Bbb A^n$ is provided as a degenerated case of a manifold with a connection and its more general case corresponding to the general relativity theory will be considered later in the book. This subject is much more advanced than a basic knowledge of affine spaces and need a much more advanced background from differential geometry and tensor analysis.

Remark. I disagree with the author’s claims that a description of space by $\Bbb R^3$ has no physical counterpart. The origin $(0,0,0)$ of $\Bbb R^3$ naturally corresponds to an origin of a chosen reference frame. Also elements of $\Bbb R^3$ can be considered as vectors with coordinatewise addition and scalar multiplication, so $\Bbb R^3$ has a natural vector space structure.

Answer 2

First let me sketch an alternative proof of the lemma, which may provide some insight:

Given any pair of lines $l_1$ and $l_2$, there is a line $l_0$ that meets both lines and is not parallel to the planes $H_i$. For example, you could take $l_0:=x_1(l_1)x_2(l_2)$, assuming that $H_1\neq H_2$ as otherwise the lemma fails. Then $l_0$ and $l_1$ are coplanar, and $l_0$ and $l_2$ are coplanar, and so it suffices to show that the ratio does not depend on $l$ in these planes. That is, it suffices to prove the claim in dimension 2, for which we can draw a picture:

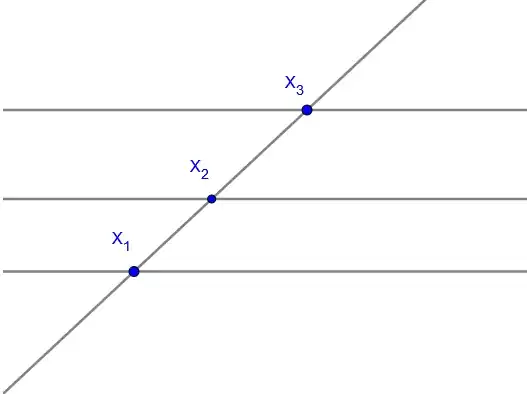
This simple case is of course an elementary exercise.

---

As for the proof in the book: First observe that the definition of $\frac{x_3-x_1}{x_2-x_1}$ makes no sense if $x_1=x_2$, and hence that the statement of the lemma makes no sense if $H_1=H_2$. The notation $\frac{x_3-x_1}{x_2-x_1}$ is also very misleading as it suggests some algebraic properties of (differences of) vectors, which they don't have. This is illustrated by some confusion in the proof itself, which contains the expression $$\frac{\pi(x_3(l))-\pi(x_1(l))}{\pi(x_2(l))-\pi(x_1(l))}.$$ This fails to make sense for some line $l$ even if $x_1(l)\neq x_2(l)$ and $H_1\neq H_2$.

As for your questions about the notation:

As you can see, the author uses projection maps $\pi$ and $\vec\pi$ but no definitions of these maps have been given.

This is not true; the author defines these maps in the same sentence where he first mentions them (emphasis mine):

This space has a natural affine structure with associated vector space $\Bbb{R}^n/\vec H$ given by $\pi(x)-\pi(z)=\vec\pi(x-z)$, where $\pi$, $\vec\pi$ denote the projections to the equivalence classes.

It is slightly ambiguous which projection map is which, but given that the expression $$\pi(x)-\pi(z)=\vec\pi(x-z),$$ is supposed to be a definition of an affine structure on $\Bbb{A}^n/\vec H$, the sensible interpretation is that $\pi$ is the quotient map on $\Bbb{A}^n$ and $\vec\pi$ is the quotient map on $\Bbb{R}^n$. Explicitly, if $[x]\in\Bbb{A}^n/\vec H$ denotes the equivalence class of $x\in\Bbb{A}^n$, the quotient maps are given by \begin{eqnarray*} &&\pi:\ \Bbb{A}^n \longrightarrow \Bbb{A}^n/\vec H:\ x\ \longmapsto\ [x],\\ &&\vec\pi:\ \Bbb{R}^n \longrightarrow \Bbb{R}^n/\vec H:\ x\ \longmapsto\ x+\vec H.\\ \end{eqnarray*} The latter is the quotient map of $\Bbb{R}^n/H$, and it should be familiar to you if you have taken linear algebra. See the Wikipedia page for basic properties of this map. The only property used is that it an $\Bbb{R}$-linear map.

As the question is tagged book-recommendation, if any of the above is still unclear (either my answer or the fragment you posted), I would recommend to pick up a book on linear algebra that takes an abstract approach. I can't recommend any particular book, but in my humble opinion you should be able to flip through Linear Algebra done wrong comfortably before attempting to read your book.