Convex function supremum of countable affine function

Question

Let $I\subset\mathbb{R}$ be an interval and $\varphi:I\to\mathbb{R}$ a convex function. I know that then $\varphi(x)=\sup\{f(x):f\leq\varphi \;\;\text{and}\;\;f(y)=ay+b,\;\; a,b\in\mathbb{R}\}$. In lecture notes im reading it says that we even have (given that $\varphi$ is not affine) $\varphi(x)=\sup\{f(x):f\leq\varphi \;\;\text{and}\;\;f(y)=ay+b,\;\; a,b\in\mathbb{Q}\}$.I was wondering how to show that second statement.

Answer 1

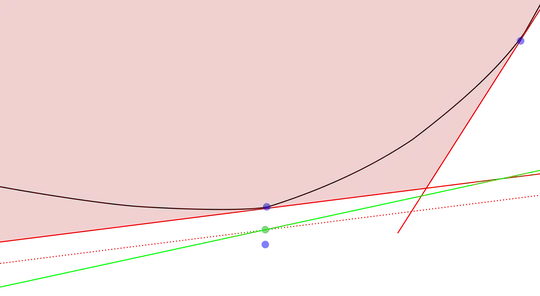
Let $$\let\phi\varphi \psi(x)=\sup\{f(x):f\leq\varphi \;\;\text{and}\;\;f(y)=ay+b,\;\; a,b\in\mathbb{Q}\}.$$ Clearly, $\psi\le\varphi$ as we take the supremum over fewer functions. Suppose $\psi(a)<\varphi(a)$. Let $\ell_a$ be a tangent to $\phi$ at $(a,\phi(a))$. As $\phi$ is not affine, there is some $b\ne a$ with $\phi(b)>\ell_a(b)$. Let $\ell_b$ be a tangent to $\phi$ at $(b,\phi(b))$. Now find a rational line $\ell$ as follows: Start with $\ell_a$; move it slightly downward to achieve $\ell(a)\in \Bbb Q$ and $\psi(a)<\ell(a)<\phi(a)$. Now rotate $\ell$ around $(a,\ell(a))$ slightly towards $\ell_b$, i.e., if $b>a$ rotate up and if $b<a$ rotate down. With a small enough rotation, we can achieve that the slope of $\ell$ is rational and $\ell$ still remains outside the shape bounded by $\ell_a$ and $\ell_b$. Now we have a rational line going above $(a,\psi(a))$, contradicting the definition of supremum.