Given disjoint circles $c_1 = \odot(P,PA), c_2 = \odot(O,OB)$ such that $B$ and $A$ are in the same half-plane wrt $OP$ and that $PA \parallel OB \perp OP$.
Line $CDQ$ is the perpendicular bisector of $AB$, $D \in AB,Q \in OP$.
Point $Q'$ is the reflection of $Q$ wrt to $M$, the midpoint of $OP$.
Point $C$ on line perpendicular to $OP$ in $Q'$.
$E = CA \cap c_1, F = CB \cap c_2$.
I want to prove $EA = FB$.
We know that $DC = DQ$ because $DM$ is midsegment of trapezium $OBAP$.
Since $BQ=AQ$ (red segments) we have $$r_1^2+(m-x)^2 = r_2^2+(m+x)^2$$ so $$p(Q',c_1)- p(Q',c_2) = \big((m+x)^2-r_1^2\big)- \big((m-x)^2-r_2^2\big) =0$$ we see that $Q'$ has equal power with respect to both circles so it lies on a radical axis which is perpendicular to $OP$ so it is $CQ'$.
Now $C$ has also equal power to both circles so $$CB\cdot CF = CA\cdot CE$$
Since $CA= CB$ we have now $CF = CE$ and we are done.
Since $OB \parallel AP$, the line $BA$ goes through the external homothetic center $X$ of the circles $(O),(P)$. The other intersections of $BA$ with the circle are $B_2,A_2$. The common external tangents also go through $X$. The points of contact of the the upper tangent are $J,K$.
The angles marked in red are all equal to $\angle{BXO}$. Let $H=B'B_2\cap OP$. $\triangle{OHB}\sim\triangle{OBX}\implies OH/OB=OB/OX\implies OH\cdot OX=OB^2\implies H$ is the inverse of $X$ wrt $(O)$. Thus $JJ'$, the polar of $X$ wrt $(O)$, contains $H$. $H'$ is the reflection of $H$ wrt $O$. $M=(O+P)/2,$ the midpoint of $O,P$.
Since $X$ is the external homothetic center, $(O)\sim (P)$. Distances of corresponding elements all have the same ratio, i.e. $XO/XP=XB/XA=XB_2/XA_2=XJ/XK$ etc. Let $h$ be the homothety that takes $(O)\rightarrow (P)$, i.e. $h(O)=P, h(B)=A$, etc.
Consider the homothety that takes a point $T$ to $(T+h(T))/2$, the midpoint of $T,h(T)$. Then, referring to the points in the OP, $O\rightarrow M, B\rightarrow (B+A)/2, H'\rightarrow Q,H\rightarrow Q',$ and $J\rightarrow M'=(J+K)/2$. But the midpoint $M'$ of $J,K$ is on the radical axis of $(O),(P)$ because the tangents from $M'$ to the two circles are of equal length. So $Q'$, which by similarity is on the line through $M'$ perpendicular to $OP$, is also on the radical axis. And so is $C$, so we are done.
Note that the bisector of $B_2,A_2$ passes through $Q'$, so this is a more direct construction.
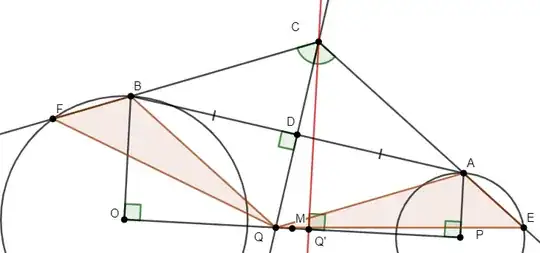
Instead of starting with $MQ'=MQ$ as a given condition, and trying to prove the equality of tangents, in order to show that $CQ'$ is the radical axis, this approach starts from the equality of tangents $LH$, $LJ$ and proves $MQ'=MQ$, and hence that $CQ'$ is the radical axis.
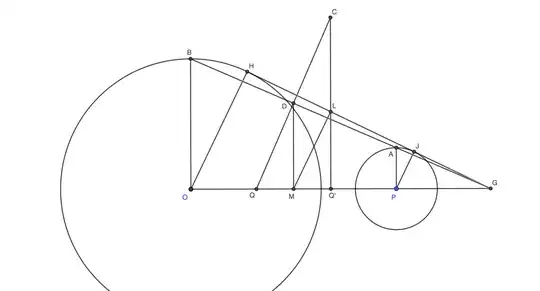
$DQ$ is perpendicular bisector of $AB$, $M$ is midpoint of $OP$, as in the posted question.
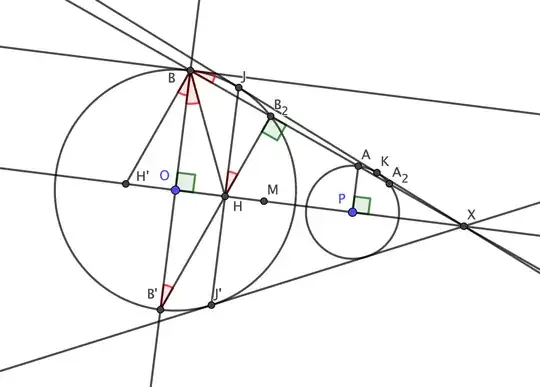
$BA$ and $OP$ extended meet at $G$. $HJ$, tangent to the circles at $H$, $J$, is known to concur with $OP$ and $BA$ at $G$.
From $L$, the midpoint of $HJ$, drop $LQ'$ perpendicular to $OP$, and extend it upward to meet $QD$ at $C$.
Join $HO$, $DM$, $ML$, $PJ$.
We prove$$QM=Q'M$$
Since $M$, $L$ bisect $OP$, $HJ$, and $OH\perp HJ$, then $$ML\perp LJ$$
Therefore$$\triangle LMQ'\sim\triangle GML\sim\triangle GOH$$and$$\triangle DQM\sim\triangle GQD\sim\triangle GBO$$But$$OH=OB$$therefore$$QM=Q'M$$
And $LH$, $LJ$ are equal tangents. Therefore $L$ lies on the radical axis.
Repeating the same construction and argument in the lower halfplane, we get a second point $L'$ on $LQ'$ extended. Therefore $CQ'$ is the radical axis.
