17

How does one calculate the homology groups of the Möbius strip?

I'm thinking of two methods.

  1. Use cellular homology. I tried to draw a delta-complex structure of the Möbius strip but I'm not sure if I'm right? I basically have a rectangle with opposite ends identified, so vertices (top-down) on the left are $a$ and $b$. On the right, they are $b$ and $a$. I know that there is an edge $e$ that joins from $b$ to $a$ and this is for both the left and right side of the rectangle. But this is not yet a delta complex structure, so I feel like I need to draw another edge across the rectangle from bottom left to top right, connecting $b$ to $b$. But how are these remaining 3 edges labelled? If I label the top and bottom edge, I think I'm creating another surface - the torus, RP2 or Klein bottle and so that's not the way to go. Does it mean this method is not possible?

  2. Use $H_n(X^k,X)$ somehow, where $X^k$ is the $k$ skeleton of $X$. But I don't quite know how to proceed with this.

Any pointers in the right direction is greatly appreciated. Thanks!

glS
  • 7,963
Haikal Yeo
  • 2,224
  • 11
    I take it you don't want to use the fact that the circle and the Mobius strip are homotopy equivalent and homology is a homotopy invariant? – Dan Rust May 11 '13 at 17:39
  • 1
    That is definitely an alternative to find the homology groups. But I'm having a question on calculating the homology groups of the Mobius strip involving it's delta-complex structure. – Haikal Yeo May 11 '13 at 17:42
  • 3
    That's perfectly fine. It's definitely a good idea to practice techniques such as these on familiar spaces, even if you have other methods for calculating these invariants. I just wanted to make sure you weren't using a a hammer to screw two pieces of wood together. – Dan Rust May 11 '13 at 17:43

3 Answers3

15

I've attached a model for the Möbius band. The vertices are $a$ and $b$. The ones that eventually get glued together are given the same letter. The edges are labeled $A$, $B$ and $C$. There are two edges labelled $A$, and they have arrows. The must be glued so that the arrows agree, i.e. you need to give a half twist before you glue. The arrows on $B$ and $C$ are only there because we must orient simplices. Finally, $\alpha$ is the one face. I don't know how to put a clockwise arrow around it, so please add one.

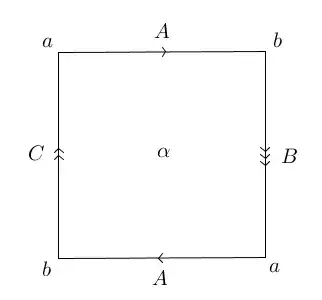
enter image description here

To find the homology groups, we must look at the images and the kernels of the boundary maps. Consider the series of maps $0 \to F \to E \to V \to 0$, where $F$ stands for faces, $E$ for edges and $V$ for vertices. In between each is a boundary map.

  • Consider $\partial : 0 \to F$. The image and the kernel are both $0$.
  • Consider $\partial : F \to E$. We have $\partial \alpha = 2A+B+C$ and so the image is non-empty. There was only one face, so the image is isomorphic to $\mathbb{Z}$. The only face had a non-zero image so the kernel is $0$.
  • Consider $\partial : E \to V$. We have $\partial A = b-a$, $\partial B = a-b$ and $\partial C = a-b$. Up to an integer, the images are all $a-b$ and so the image is one dimensional: $\mathbb{Z}$. There were three edges, and the image was one dimensional, so the kernel must be two dimensional: $\mathbb{Z}^2$.
  • Consider $\partial : V \to 0$. We have $\partial a = \partial b = 0$ and so the image is $0$. There are two vertices, and so the kernel must be $\mathbb{Z}^2.$

We can put all of this together. The group $H_2(M,\mathbb{Z})$ is given by the quotient of the kernel of $F \to E$ by the image of $0 \to F$, i.e. $0/0 \cong 0$. The group $H_1(M,\mathbb{Z})$ is given by the quotient of the kernel of $E \to V$ by the image of $F \to E$, i.e. $\mathbb{Z}^2/\mathbb{Z} \cong \mathbb{Z}$. The group $H_0(M,\mathbb{Z})$ is given by the quotient of the kernel of $V \to 0$ by the image of $E \to V$, i.e. $\mathbb{Z}^2/\mathbb{Z} \cong \mathbb{Z}$. Hence:

\begin{array}{ccc} H_2(M,\mathbb{Z}) &\cong& \{0\} \\ H_1(M,\mathbb{Z}) &\cong& \mathbb{Z} \\ H_0(M,\mathbb{Z}) &\cong& \mathbb{Z} \end{array}

Fly by Night
  • 32,886
  • 4
    I think for simplicial homology, faces must be triangles. – Haikal Yeo May 11 '13 at 21:33
  • 1
    @HaikalYeo Are my results incorrect? I used a CW-complex, which yields exactly the same homology groups. Feel free to add extra edges and extra faces and spend longer making the calculations. You'll get exactly the same groups. – Fly by Night May 11 '13 at 22:26
  • 4
    Can you elaborate on the step $\mathbb{Z}^2/\mathbb{Z} \cong \mathbb{Z}$? This doesn't make sense to me. For example, if we view $\mathbb{Z}$ as embedded in $\mathbb{Z}^2$ via $a \mapsto (2a,0)$, then the quotient will be $\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}$. – goblin GONE Jul 11 '16 at 08:54
  • @goblin The image of $\partial : F \to E$ is $\mathbb Z\langle 2A+B+C\rangle$ while the kernel of $\partial : E \to V$ is $\mathbb Z\langle A+B,A+C\rangle$. We want to find $\mathbb Z\langle A+B,A+C\rangle / \mathbb Z\langle 2A+B+C\rangle$. Notice that $(A+B)+(A+C)=2A+B+C$ and so $(A+B)+(A+C) \equiv 0$. $\mathbb Z\langle A+B,A+C\rangle$ has two generators, but they are linearly dependent, so there is only one linearly independent generator. Hence $\mathbb Z\langle A+B,A+C\rangle / \mathbb Z\langle 2A+B+C\rangle \cong \mathbb Z^1$ – Fly by Night Jul 18 '16 at 16:41
  • May I ask when can we compute the CW-complex pretending it is a simplicial complex like @Fly by Night , and when cannot? – N.Li Sep 06 '23 at 08:52
11

Take the usual paper strip that you would glue to make a Möbius strip. If you want to get a simplicial complex, draw a line diagonally from the top corner on the left to the bottom corner on the right, so your paper strip is a union of two triangles.

Your strip now has two triangular faces, five 1-simplices (the four edges of the paper strip, together with the line you drew to divide it into two triangles), and 4 vertices. But when you glue you identify the two edges at either end of the strip, so for the Möbius band there are two faces, four 1-simplices, and 2 vertices.

Now just write down the corresponding simplicial chain complex and compute away!

azimut
  • 24,316
Matt E
  • 127,227
11

A slick way of calculating the homology groups here is to notice that the Möbius strip is homotopy equivalent to $S^1$. Then you can apply Corollary 2.11 (Section 2.1) of Hatcher that:

The maps $\ f_{\ast} : H_n(X) \rightarrow H_n(Y)$ induced by a homotopy equivalence $ \ f : X \rightarrow Y$ are isomorphisms for all $n$.

This should make the task much easier.

cbishop
  • 659