12

I would like to prove the following inequalities on Laguerre polynomials evaluated at point 2: $$ (-1)^n \text{Laguerre}_n(2) \leq 1 $$ This seems to hold numerically. I tried to use the recurrence relation between Laguerre polynomials but I was not successful. Any ideas? I also tried expression via Bessel function $J_0$ and then contour integral but it was not successful.

GNUSupporter 8964民主女神 地下教會
  • 17,998
Plussoyeur
  • 335
  • This seems hard. There is a clasic bound due to Szego that in your case gives $|L_n(2)|\leq e.$ – Phicar Oct 28 '20 at 18:37
  • This has Szego result stated and some better results. https://www.sciencedirect.com/science/article/pii/S0021904506000700 But not good for the exact problem you posted. – Phicar Oct 28 '20 at 19:01
  • Yes this indeed seems hard but it also seems true. I've seen those bounds but not helpful sadly. – Plussoyeur Oct 29 '20 at 08:23

2 Answers2

7

Theorem 8.22. on Szego's Orthogonal polynomials the asymptotics of the Laguerre polynomials (called there Fejer's formula) looks like $$L_n(x)=\frac{e^{x/2}}{2^{1/4}\sqrt{\pi}\cdot n^{1/4}}cos \left ( 2\sqrt{nx}-\pi /4\right )+O(n^{-3/4}),\, \text{for }x>0.$$ Take $x=2,$ we have then that $$|L_n(2)|\leq \frac{e}{2^{1/4}\sqrt{\pi}}\left |\frac{cos(2^{3/2}\sqrt n-\pi /4)}{n^{1/4}} \right |+\left |O(n^{-3/4})\right |\leq 1.2896\cdot \frac{1}{n^{1/4}}+\frac{C}{n^{3/4}},$$ for some constant $C.$

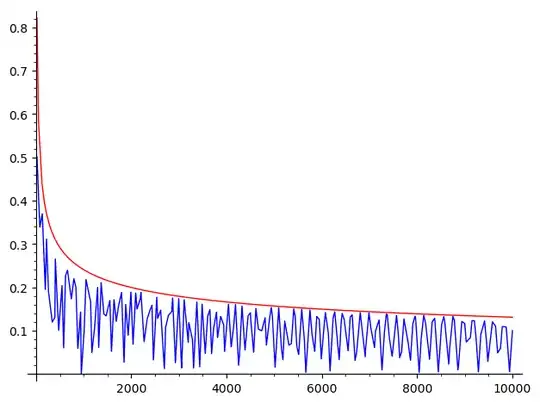
Even if the constant is something big, you can check the result for small values of $n.$ Here is a graph using $C=2$ which I would say is big according to simulation: enter image description here

Also, this is a very good survey about the whole problem

Phicar
  • 14,827
  • Thanks a lot for your answer. If was hoping for an analytical proof but I guess I can also rely on numerical analysis. – Plussoyeur Nov 04 '20 at 08:47
  • @Plussoyeur Not entirely sure what you mean. Fejer's formula certainly is an analytical result. So for sure, from some point $n_0$ you have your identity. Now, simulation suggests that $n_0$ is not very big, but I have not seen the proof for Fejer's. Perhaps going thru that will light in how is the asymptotic expression found. – Phicar Nov 04 '20 at 12:39
  • 1
    No right I meant the tuning of C and finding $n_0$. – Plussoyeur Nov 04 '20 at 13:04
1

Plot of the function

This is a graph of $(-1)^n L_{n}^{(0)}(2)$ where $0 \leq n \leq 2500$. In this range $|(-1)^n L_{n}^{(0)}(2)| \leq 1$. This may be of interest. The Digital Library of Mathematical Functions, NIST gives $| L_{n}^{(0)}(2)| \leq e$ in equation 18.14.8 as above. Proving a better bound is probably difficult.

DavidW
  • 572
  • Indeed I don't know what more can be done. But the bound is for all $x$ so I'm sure something more can be done. Maybe some recurrence relation... – Plussoyeur Oct 29 '20 at 08:24
  • 2
    I'm calling it Plussoyeur's Conjecture, – DavidW Oct 29 '20 at 09:29
  • A bounty of 50 reputation is available on Math Stack Exchange for anyone able to solve the Plussoyeur's Conjecture. Is it attractive enough? – Plussoyeur Oct 29 '20 at 09:44
  • Remind me to give you this bounty if no one provides an answer by tomorrow... – Plussoyeur Nov 03 '20 at 13:27
  • What was the context for the question? An answer would be a proof. According to Wikipedia, $(-1)^{n-i} L_{n-i}(x)$ where $0 \leq i \leq n$ is a Sturm Chain which may be relevant. – DavidW Nov 04 '20 at 10:20
  • Rather complicated. Comes from an infinite linear program. I found an analytical solution provided this holds. What do you mean "an answer would be a proof" ? – Plussoyeur Nov 04 '20 at 10:45
  • Simply that the question stated "I would like to prove .." . That context is unexpected. – DavidW Nov 04 '20 at 10:58
  • No proof sadly but at least the bounty did not disappear in the air. – Plussoyeur Nov 04 '20 at 12:02
  • Thanks for an intriguing problem. I will still think about solving it. The bounty is appreciated, and Phicar provided more precise information. – DavidW Nov 04 '20 at 12:11
  • I hesitated with Phicar but then he has so much reputation already. Felt you needed it more. – Plussoyeur Nov 04 '20 at 13:02