let $f:[0,1]\longrightarrow R $ be a continuous function, if $$\int_{0}^{1}x^2f(x)dx=-2\int_{\frac{1}{2}}^{1}F(x)dx$$ where $F(x)=\displaystyle\int_{0}^{x}f(t)dt,x\in [0,1]$,then prove that $$\int_{0}^{1}f^2(x)dx\ge 24\left(\int_{0}^{1}f(x)dx\right)^2$$
I think this inequality is very interesting, becasue not long ago,I have solve this a little same problem:Funny integral inequality
I believe this two problem have same methods.Thank you everyone
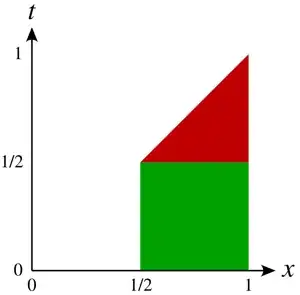
We start with, $\displaystyle \int_{\frac{1}{2}}^1 F(x)\,dx = \int_{\frac12}^1\int_0^x f(t)\,dt \,dx = \frac{1}{2}\int_0^{\frac12} f(x)\,dx + \int_{\frac12}^1 (1-x)f(x)\,dx$
Thus we have, $$\displaystyle \int_0^1 x^2f(x)\,dx = -\int_0^{\frac12}f(x)\,dx - 2\int_{\frac12}^1 (1-x)f(x)\,dx$$
and, $$\displaystyle \int_0^1 f(x)\,dx = -\int_{\frac12}^1 (x-1)^2f(x)\,dx - \int_0^{\frac12} x^2f(x)\,dx$$
Hence, $\displaystyle \int_{\frac12}^1 \{1+(x-1)^2\}f(x)\,dx + \int_0^{\frac12} \{1+x^2\}f(x)\,dx = 0$
Say, $\phi(x) = 1+x^2 \textrm{ for } x \in [0,\frac12) \textrm{ and } 1+(x-1)^2 \textrm{ for } x \in [\frac12,1]$
Then, $\displaystyle \int_0^1 \phi(x)f(x)\,dx = 0$
Now by Cauchy-Schwarz Inequality :
$\displaystyle \left(\int_0^1 f(x)\,dx \right)^2 = \left(\int_0^1 f(x) + m\phi(x)f(x)\,dx \right)^2 \le \left(\int_0^1 f^2(x)\,dx\right)\left(\int_0^1 (1+m\phi(x))^2\,dx\right)$
Since, $\displaystyle \int_0^1 (1+m\phi(x))^2\,dx = 1 + \frac{13}{6}m +\frac{283}{240}m^2 \ge \frac{4}{849}$
We have, $\displaystyle \left(\int_0^1 f(x)\,dx \right)^2 \le \frac{4}{849}\int_0^1 f^2(x)\,dx$
The constant $\frac{4}{849}$ is the best possible since equality is attained for $f(x) = 1- \frac{260}{283}\phi(x)$.
We have $$ \begin{align} \int_{1/2}^1F(x)\,\mathrm{d}x &=\int_{1/2}^1\int_0^xf(t)\,\mathrm{d}t\,\mathrm{d}x\\ &=\color{#00A000}{\int_0^{1/2}\int_{1/2}^1f(t)\,\mathrm{d}x\,\mathrm{d}t}+\color{#C00000}{\int_{1/2}^1\int_t^1f(t)\,\mathrm{d}x\,\mathrm{d}t}\\ &=\int_0^{1/2}\frac12f(t)\,\mathrm{d}t+\int_{1/2}^1(1-t)f(t)\,\mathrm{d}t\\ &=-\frac12\int_0^1t^2f(t)\,\mathrm{d}t\tag{1} \end{align} $$ since we are integrating $f(t)$ over the following region in $\mathbb{R}^2$
$\hspace{5cm}$
Rearranging $(1)$, we have $$ \int_0^{1/2}\frac{t^2+1}{2}f(t)\,\mathrm{d}t+\int_{1/2}^1\frac{(1-t)^2+1}{2}f(t)\,\mathrm{d}t=0\tag{2} $$ Aside from a scale factor, we want to minimize $$ \int_0^1f(t)^2\,\mathrm{d}t\tag{3} $$ given $$ \int_0^1f(t)\,\mathrm{d}t=1\tag{4} $$ That means for every variation $\delta f$ so that $(2)$ and $(4)$ hold, that is, $$ \int_0^{1/2}\frac{t^2+1}{2}\delta f(t)\,\mathrm{d}t+\int_{1/2}^1\frac{(1-t)^2+1}{2}\delta f(t)\,\mathrm{d}t=0\tag{5} $$ and $$ \int_0^1\delta f(t)\,\mathrm{d}t=0\tag{6} $$ we have $(3)$ is stationary, that is, $$ \int_0^1f(t)\delta f(t)\,\mathrm{d}t=0\tag{7} $$ Orthogonality says that there must be constants $\mu$ and $\lambda$ so that $$ f(t)=\mu\cdot1+\lambda\left(\frac{t^2+1}{2}[0\le t\le1/2]+\frac{(1-t)^2+1}{2}[1/2\le t\le1]\right)\tag{8} $$ Plugging $(8)$ into $(2)$ says $$ \frac{13}{24}\mu+\frac{283}{960}\lambda=0\tag{9} $$ Plugging $(8)$ into $(4)$ says $$ \mu+\frac{13}{24}\lambda=1\tag{10} $$ Solving $(9)$ and $(10)$ gives $$ \mu=\frac{849}{4}\qquad\text{and}\qquad\lambda=-390\tag{11} $$ Plugging $(8)$ and $(11)$ into $(3)$ yields $$ \int_0^1f(t)^2\,\mathrm{d}t=\frac{849}{4}\tag{12} $$ Squaring $(4)$, to make things homogeneous, allows us to say $$ \int_0^1f(t)^2\,\mathrm{d}t\ge\frac{849}{4}\left(\int_0^1f(t)\,\mathrm{d}t\right)^2\tag{13} $$
Thought：by Cauchy-Schwarz inequality, $$\bigg(\int_0^1g(x)f(x)\,\mathrm{d} x\bigg)^2\leqslant\int_0^1g^2(x)\,\mathrm{d} x\int_0^1f^2(x)\,\mathrm{d} x$$ We just need to prove that there is a constant K. $$\int_0^1g(x)f(x)\,\mathrm{d} x=K\int_0^1f(x)\,\mathrm{d} x$$ Proof. by integration by parts, \begin{align*} -2\int_{\frac{1}{2}}^{1}F(x)\,\mathrm{d} x&=\int_{\frac{1}{2}}^{1}F(x)\,\mathrm{d}(C-2x) =(C-2x)F(x)\bigg|_{\frac{1}{2}}^1+\int_{\frac{1}{2}}^{1}(2x-C)f(x)\,\mathrm{d} x\\ &=\int_0^1(C-2)f(x)\,\mathrm{d} x+\int_0^{\frac{1}{2}}(1-C)f(x)\,\mathrm{d} x+\int_{\frac{1}{2}}^{1}(2x-C)f(x)\,\mathrm{d} x \end{align*} Since $\textstyle\int_0^1x^2f(x)\,\mathrm{d} x=-2\int_{\frac{1}{2}}^{1}F(x)\,\mathrm{d} x$, $$\int_0^1(C-2)f(x)\,\mathrm{d} x=\int_0^{\frac{1}{2}}(x^2+C-1)f(x)\,\mathrm{d} x+\int_{\frac{1}{2}}^{1}(C-2x+x^2)f(x)\,\mathrm{d} x$$ Consequently, let $$g(x)=\begin{cases} x^2+C-1,& x\in[0,\tfrac{1}{2})\\ C-2x+x^2,& x\in[\tfrac{1}{2},1) \end{cases}$$ by Cauchy-Schwarz inequality, \begin{align*} \left(\int_0^1(C-2)f(x)\,\mathrm{d} x\right)^2&=(C-2)^2\left(\int_0^1f(x)\,\mathrm{d} x\right)^2=\left(\int_0^1g(x)f(x)\,\mathrm{d} x\right)\\ &\leqslant\int_0^1g^2(x)\,\mathrm{d} x\int_0^1f^2(x)\,\mathrm{d} x \end{align*} After calculation, we get $$\int_0^1g^2(x)\,\mathrm{d} x=\frac{240c^2-440c+203}{240}$$ Hence, we have $$\left(\int_0^1f(x)\,\mathrm{d} x\right)^2\leqslant\frac{240c^2-440c+203}{240(C-2)^2}\int_0^1f^2(x)\,\mathrm{d} x$$ Let $h(C)=\frac{240C^2-440C+203}{240(C-2)^2}\Rightarrow \lim_{C\to2}h(C)=+\infty$ $$h'(C)=\frac{237-260C}{120(C-2)^3} \Leftrightarrow h'(C)=0\Rightarrow C=\frac{237}{260}\Rightarrow h(\tfrac{237}{260})=\frac{4}{849}$$ $$\begin{array}{cccccc} \hline & (-\infty,\tfrac{237}{260}) & \tfrac{237}{260} & (\tfrac{237}{260},2) & (2,+\infty) & +\infty\\\hline h'(C) & <0 & 0 & >0 & <0 & <0 \\ h(C) & \downarrow & \text{local minimum} & \uparrow & \downarrow & 1\\\hline \end{array}$$ So, we have $$\min_{C\neq2}h(C)=h(\tfrac{237}{260})=\frac{4}{849}$$ Therefore, $$\int_0^1f^2(x)\,\mathrm{d} x\geqslant\frac{849}{4}\bigg(\int_0^1f(x)\,\mathrm{d} x\bigg)^2$$ Obviously, $\tfrac{849}{4}$ is the best constant, the equality holds if and only if $C=\frac{237}{260}$ and $f(x)=g(x)$
Here is another method to get an inequality such as the OP's.
As @robjohn pointed out by an application of Fubini's theorem
$$\int_0^1t^2f(t)\,\mathrm{d}t=-\int_0^{1/2}f(t)\,\mathrm{d}t+\int_{1/2}^12(t-1)f(t)\,\mathrm{d}t\tag{1} $$ This can be written as $$\int^1_0 g(t) f(t)\,dt=0$$ where $g(t)=t^2+\mathbb{1}_{[0,1/2]}(t)-2(t-1)\mathbb{1}_{(1/2,1]}(t)$. Now, $$\int^1_0g(t)\,dt=\int^{1/2}_0(t^2+1)\,dt +\int^1_{1/2}(t^2-2t+2)\,dt=\frac{13}{12} $$ and $$\int^1_0g^2(t)\,dt=\int^{1/2}_0(t^2+1)^2\,dt +\int^1_{1/2}(t^2-2t+2)^2\,dt=\frac{283}{240}$$
Here is a general result that can be formulated in the context of Bessel's inequality and Parseval's indentity in Hilbert spaces.
Lemma: Let $(X,\mathscr{F},\mu)$ be a measure space. Suppose $f,g\in L_2(\mu)$, $\|f\|_2\|g\|_2>0$. If $\int_X fg=0$, then for any $h\in L_2(\mu)$ $$\frac{\Big(\int_X fh\Big)^2}{\int_X f^2 }+\frac{\Big(\int_X hg\Big)^2}{\int_X g^2 }≤\int_Xh^2\tag{2}\label{two}$$
Thus, if $\int^1_0f^2(t)\,dt>0$, an application of the Lemma above with $h\equiv1$ yields $$ \frac{\left(\int^1_0 f(t)\,dt\right)^2}{\int^1_0 f^2(t)\,dt}+\frac{169}{144}\frac{240}{283}\leq 1 $$ That is, $$ \frac{\left(\int^1_0 f(t)\,dt\right)^2}{\int^1_0 f^2(t)\,dt}\leq \frac{4}{849} $$ or equivalently $$\int^1_0f^2(t)\,dt\geq \frac{849}{4}\left(\int^1_0f(t)\,dt\right)^2$$
Proof of Lemma: Without loss of generality, we may assume that $\|f\|_2=\|g\|_2=1=\|h\|_2$. Then, for all $a\in\mathbb{R}$, \begin{align} \left(\int fh\right)^2&=\Big(\int f(h+ag)\Big)^2\leq\int(h+ag)^2\\ &=1+2a\int hg + a^2=\phi(a) \end{align} The function $\phi(a)$ is minimized at $a_*=-\int gh$, and $\phi(a_*)=1-\int hg$. Inequality \eqref{two} follows.
