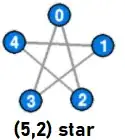
Let us define a $(n,m)$-star as a graph with the set of nodes $\mathbb{Z_n}=\{0,1,...,n\}$ and set of edges $\{\{x,x+m\} : x \in \mathbb{Z_n}\}$ (sum calculated in $\mathbb{Z_n}$).
Example graph:
For which $ 0 <m <n $ does a $(n,m)$ star become connected? Find an expression for the number of connected components in a $(n,m)$ star.
I tried experimenting with different stars but have not been able to gain any important information from them. To give an example, I created the stars $(6,2), (6,3), (6,4), (6,5)$ and found the following:
$n=6$ and $1 \leq m \leq 6$
Star $(6,1)$ is connected and has 1 connected component.
$$Edges: [(0,1),(1,2),(2,3),(3,4),(4,5),(5,0)]$$
Star $(6,2)$ is not connected and has 2 connected components.
$$Edges: [(0,2),(1,3),(2,4),(3,5),(4,0),(5,1)]$$
Star $(6,3)$ is not connected and has 3 connected components.
$$Edges: [(0,3),(1,4),(2,5)]$$
Star $(6,4)$ is not connected and has 2 connected components.
$$Edges: [(0,4),(1,5),(2,0),(3,1),(4,2),(5,3)]$$
Star $(6,5)$ is connected and has 1 connected component.
$$Edges: [(0,5),(1,0),(2,1),(3,2),(4,3),(5,4)]$$
Star $(6,6)$ is connected and has 6 connected components.
$$Edges: [(0,0),(1,1),(2,2),(3,3),(4,4),(5,5)]$$
I seem to have found that for every star $(n,m)$, the difference between the pair of vertices $(v_i,v_j)$ is always equal to $m$ mod $n$.
For example for $n=6$ and $1 \leq m \leq 6$, I get the above listed sets of edges. Let's take one of those lists, say for the star $(6,5)$. The list is $$Edges: [(0,5),(1,0),(2,1),(3,2),(4,3),(5,4)]$$
If we compute:
$$ (5-0)=5\pmod{6} = 5 = n-1 $$
$$ (0-1)=-1\pmod{6}= 5 = n-1 $$
$$ (1-2)=-1\pmod{6}= 5 = n-1 $$
$$ (2-3)=-1\pmod{6}= 5 = n-1 $$
$$ (3-4)=-1\pmod{6}= 5 = n-1 $$
$$ (4-5)=-1\pmod{6}= 5 = n-1 $$
I still don't see any connection to my original question even with this new discovery of mine. It would help to be able to know if each generated graph is connected or not without having to manually evaluate that. I do not know how to do that via coding. Maybe that'd help me see some other pattern.
Here is the same computation but with different $n$ and $1 \leq m \leq n$
-- calcDiffPairEdge (lowerBound, n)
-- lowerBound <= m <= n
*Main> calcDiffPairEdge (1,1)
m=1 [0]
*Main> calcDiffPairEdge (1,2)
m=1 [1]
m=2 [0,0]
*Main> calcDiffPairEdge (1,3)
m=1 [1,1,1]
m=2 [2,2,2]
m=3 [0,0,0]
*Main> calcDiffPairEdge (1,4)
m=1 [1,1,1,1]
m=2 [2,2]
m=3 [3,3,3,3]
m=4 [0,0,0,0]
*Main> calcDiffPairEdge (1,5)
m=1 [1,1,1,1,1]
m=2 [2,2,2,2,2]
m=3 [3,3,3,3,3]
m=4 [4,4,4,4,4]
m=5 [0,0,0,0,0]
*Main> calcDiffPairEdge (1,6)
m=1 [1,1,1,1,1,1]
m=2 [2,2,2,2,2,2]
m=3 [3,3,3]
m=4 [4,4,4,4,4,4]
m=5 [5,5,5,5,5,5]
m=6 [0,0,0,0,0,0]
*Main> calcDiffPairEdge (1,7)
m=1 [1,1,1,1,1,1,1]
m=2 [2,2,2,2,2,2,2]
m=3 [3,3,3,3,3,3,3]
m=4 [4,4,4,4,4,4,4]
m=5 [5,5,5,5,5,5,5]
m=6 [6,6,6,6,6,6,6]
m=7 [0,0,0,0,0,0,0]
*Main> calcDiffPairEdge (1,8)
m=1 [1,1,1,1,1,1,1,1]
m=2 [2,2,2,2,2,2,2,2]
m=3 [3,3,3,3,3,3,3,3]
m=4 [4,4,4,4]
m=5 [5,5,5,5,5,5,5,5]
m=6 [6,6,6,6,6,6,6,6]
m=7 [7,7,7,7,7,7,7,7]
m=8 [0,0,0,0,0,0,0,0]
*Main> calcDiffPairEdge (1,9)
m=1 [1,1,1,1,1,1,1,1,1]
m=2 [2,2,2,2,2,2,2,2,2]
m=3 [3,3,3,3,3,3,3,3,3]
m=4 [4,4,4,4,4,4,4,4,4]
m=5 [5,5,5,5,5,5,5,5,5]
m=6 [6,6,6,6,6,6,6,6,6]
m=7 [7,7,7,7,7,7,7,7,7]
m=8 [8,8,8,8,8,8,8,8,8]
m=9 [0,0,0,0,0,0,0,0,0]
*Main> calcDiffPairEdge (1,10)
m=1 [1,1,1,1,1,1,1,1,1,1]
m=2 [2,2,2,2,2,2,2,2,2,2]
m=3 [3,3,3,3,3,3,3,3,3,3]
m=4 [4,4,4,4,4,4,4,4,4,4]
m=5 [5,5,5,5,5]
m=6 [6,6,6,6,6,6,6,6,6,6]
m=7 [7,7,7,7,7,7,7,7,7,7]
m=8 [8,8,8,8,8,8,8,8,8,8]
m=9 [9,9,9,9,9,9,9,9,9,9]
m=10 [0,0,0,0,0,0,0,0,0,0]
*Main> calcDiffPairEdge (1,11)
m=1 [1,1,1,1,1,1,1,1,1,1,1]
m=2 [2,2,2,2,2,2,2,2,2,2,2]
m=3 [3,3,3,3,3,3,3,3,3,3,3]
m=4 [4,4,4,4,4,4,4,4,4,4,4]
m=5 [5,5,5,5,5,5,5,5,5,5,5]
m=6 [6,6,6,6,6,6,6,6,6,6,6]
m=7 [7,7,7,7,7,7,7,7,7,7,7]
m=8 [8,8,8,8,8,8,8,8,8,8,8]
m=9 [9,9,9,9,9,9,9,9,9,9,9]
m=10 [10,10,10,10,10,10,10,10,10,10,10]
m=11 [0,0,0,0,0,0,0,0,0,0,0]
*Main> calcDiffPairEdge (1,12)
m=1 [1,1,1,1,1,1,1,1,1,1,1,1]
m=2 [2,2,2,2,2,2,2,2,2,2,2,2]
m=3 [3,3,3,3,3,3,3,3,3,3,3,3]
m=4 [4,4,4,4,4,4,4,4,4,4,4,4]
m=5 [5,5,5,5,5,5,5,5,5,5,5,5]
m=6 [6,6,6,6,6,6]
m=7 [7,7,7,7,7,7,7,7,7,7,7,7]
m=8 [8,8,8,8,8,8,8,8,8,8,8,8]
m=9 [9,9,9,9,9,9,9,9,9,9,9,9]
m=10 [10,10,10,10,10,10,10,10,10,10,10,10]
m=11 [11,11,11,11,11,11,11,11,11,11,11,11]
m=12 [0,0,0,0,0,0,0,0,0,0,0,0]
I think I have found the patterns.
If $n$ is a prime number then all the stars of the form $(n,m)$ where $1 < m < n$ will be connected.
If $n$ is not a prime number then all stars of the form $(n,m)$ will have $gcd(n,m)$ number of connected components. Meaning if $n$ is not prime and $gcd(n,m)$ = 1 then we will have a connected graph. If $gcd(n,m)=c \neq 1$ we will get $c$ connected graphs.