I'm working on a project to do with bouncing rays inside polygons and now I've reached a crucial stage of this project in which I need help with and is related to the problem stated below. Your help will be highly appreciated.
$\\$
Problem
Let $P_n$ be a polygon such that if I shoot a ray from some point inside the polygon at a certain angle and I let the ray bounce off the edges continuously, I'll have at least one point $p$ inside the polygon with exactly $n$ rays (with different slopes) going through such point. We can refer to such polygon as a $P_n$-polygon. Does a $P_n$-polygon exist for every $n\geq 3?$ And if so, is such polygon also a $P_0, P_1,...,P_{n-1}$ polygon$?$
$\\$
(A square is an example of a $P_0,P_1$ and $P_2$-polygon depending on the position and the angle I shoot the ray from, inside the square.)
$\\$
UPDATE: $\\$
Based on a comment below and after some tries, here's an example of a $P_0, P_1, P_2$ and $P_3$-Polygon.
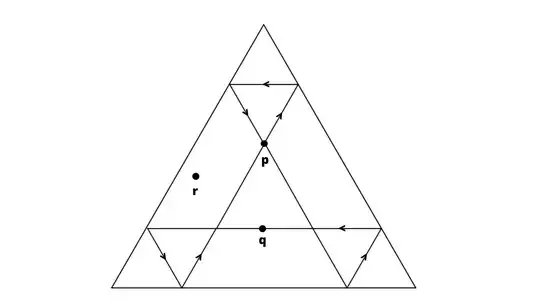
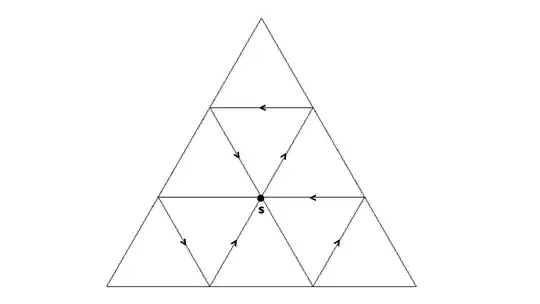
In the first picture, if we choose $p$ as the starting point to shoot the ray from, inside the equilateral triangle, we can see that after the reflections the ray goes through $p$ from two different angles (slopes). The ray goes through point $q$, from only one angle (slope) and it never goes through $r$. As for the second picture we can see that using $s$ as the starting point, the ray goes through it from three different angles (slopes). Hence an equilateral triangle is an example of a $P_0, P_1, P_2$ and $P_3$-polygon.
$\\$ Whilst this is not a proof for the general case hopefully it should give some indication as to how to approach it.