I think that this inequality is strong, though I do not have knowledge of many techniques. There goes my work:
Positive variables only make the inequality stronger, hence suppose $a,b,c\geqslant0$
$$
\sqrt{a^2+5b^2}+\sqrt{b^2+5c^2}+\sqrt{c^2+5a^2}\geqslant\sqrt{10(a^2+b^2+c^2)+8(ab+ac+bc)}
$$By squaring,
$$
\Rightarrow
\sqrt{(a^2+5b^2)(b^2+5c^2)}+\sqrt{(b^2+5c^2)(c^2+5a^2)}+\sqrt{(c^2+5a^2)(a^2+5b^2)}\geq2(a+b+c)^2
$$The $LHS$
$$=
\sqrt{\sum_{cyc}{5b^4 + 31a^2b^2 + 2\left(a^2 + 5b^2\right) \left(\sqrt{\left(b^2 + 5c^2\right) \left(c^2 + 5a^2\right)}\right)}}
$$$$
\geqslant
\sqrt{\sum_{cyc}{5b^4 + 31a^2b^2 + 2(a^2 + 5b^2)(bc + 5ca)}}
$$
Now we are only left to prove that
$$
\sum_{cyc}{5b^4 + 31a^2b^2 + 52a^2bc + 10a^3c + 10a^3c} \geqslant \sum_{cyc}{4a^4 + 16(a^3b + ab^3) + 24a^2b^2 + 48a^2bc}
$$$$
\sum_{cyc}{a^4 + 7a^2b^2 + 4a^2bc - 6(a^3b + ab^3)} \geqslant 0
$$
The last inequality is wrong for $(a,b,c) = (1,1,0)$. Cauchy Schwarz looks fine but I am not able to find a way.
I found this inequality posted by arqady on aops forum.
Please help!
- 203,855
- 1,536
3 Answers
Since $x\leq|x|$, it's enough to prove our inequality for non-negative variables.
Now, after squaring of the both sides we need to prove that $$\sum_{cyc}\sqrt{(a^2+5b^2)(b^2+5c^2)}\geq2(a+b+c)^2.$$ Also, $$\sum_{cyc}\sqrt{(a^2+5b^2)(b^2+5c^2)}=$$ $$=\sqrt{\sum_{cyc}\left((a^2+5b^2)(b^2+5c^2)+2(c^2+5a^2)\sqrt{(a^2+5b^2)(b^2+5c^2)}\right)}=$$ $$=\sqrt{\sum_{cyc}\left(5a^4+31a^2b^2+2\sqrt{\prod_{cyc}(a^2+5b^2)}\sqrt{a^2+5b^2}\right)}=$$ $$=\sqrt{\sum_{cyc}(5a^4+31a^2b^2)+2\sqrt{\prod_{cyc}(a^2+5b^2)}\sqrt{\sum_{cyc}\left(6a^2+2\sqrt{(a^2+5b^2)(b^2+5c^2)}\right)}}.$$ But by C-S $$2\sum_{cyc}\sqrt{(a^2+5b^2)(b^2+5c^2)}=$$ $$=\frac{1}{3}\sum_{cyc}\sqrt{((a+5b)^2+5(a-b)^2)((b+5c)^2+5(b-c)^2)}\geq$$ $$\geq\frac{1}{3}\sum_{cyc}((a+5b)(b+5c)+5(b-a)(b-c)).$$ Id est, it's enough to prove that: $$\sum_{cyc}(5a^4+31a^2b^2)+2\sqrt{\frac{1}{3}\prod_{cyc}(a^2+5b^2)\sum_{cyc}(28a^2+26ab)}\geq4(a+b+c)^4$$ or $$2\sqrt{\frac{1}{3}\prod_{cyc}(a^2+5b^2)\sum_{cyc}(28a^2+26ab)}\geq4(a+b+c)^4-\sum_{cyc}(5a^4+31a^2b^2),$$ which is obvious for $$4(a+b+c)^4-\sum_{cyc}(5a^4+31a^2b^2)<0.$$ Thus, it's enough to prove our inequality for $$4(a+b+c)^4-\sum_{cyc}(5a^4+31a^2b^2)\geq0.$$ Now, let $a=\min\{a,b,c\}$, $b=a+u$ and $c=a+v$.
Thus, we need to prove that: $$8\prod_{cyc}(a^2+5b^2)\sum_{cyc}(14a^2+13ab)\geq3\left(4(a+b+c)^4-\sum_{cyc}(5a^4+31a^2b^2)\right)^2,$$ for which it's enough to prove that: $$8\prod_{cyc}(a^2+5b^2)\sum_{cyc}(14a^2+13ab)-3\left(4(a+b+c)^4-\sum_{cyc}(5a^4+31a^2b^2)\right)^2\geq$$ $$\geq4\left(u^2-5uv+v^2\right)^2\left(4(a+b+c)^4-\sum_{cyc}(5a^4+31a^2b^2)\right ).$$ Now, $$8\prod_{cyc}(a^2+5b^2)\sum_{cyc}(14a^2+13ab)-3\left(4(a+b+c)^4-\sum_{cyc}(5a^4+31a^2b^2)\right)^2=$$ $$=19008(u^2-uv+v^2)a^6+5184(4u^3-5u^2v+15uv^2+4v^3)a^5+$$ $$+144(109u^4-458u^3v+867u^2v^2+742uv^3+109v^4)a^4+$$ $$+64(114u^5-677u^4v+529u^3v^2+2399u^2v^3+1088uv^4+114v^5)a^3+$$ $$+4(438u^6-2978u^5v+107u^4v^2+13656u^3v^3+20467u^2v^4+5822uv^5+438v^6)a^2+$$ $$+4(42u^7-269u^6v-191u^5v^2+2403u^4v^3+5523u^3v^4+5249u^2v^5+851uv^6+42v^7)a-$$ $$-3u^8+96u^7v-250u^6v^2+1288u^5v^3+1671u^4v^4+3368u^3v^5+1990u^2v^6+96uv^7-3v^8.$$ Also, $$4(a+b+c)^4-\sum_{cyc}(5a^4+31a^2b^2)=$$ $$=216a^4+288(u+v)a^3+4(31u^2+77uv+31v^2)a^2+$$ $$+(28u^3+82u^2v+82uv^2+28v^3)a-u^4+16u^3v-7u^2v^2+16uv^3-v^4.$$ Easy to see that $$19008(u^2-uv+v^2)\geq19008uv,$$ $$5184(4u^3-5u^2v+15uv^2+4v^3)\geq80899\sqrt{u^3v^3},$$ $$144(109u^4-458u^3v+867u^2v^2+742uv^3+109v^4)-$$ $$-4\left(u^2-5uv+v^2\right)^2\cdot216\geq99373u^2v^2,$$ $$64(114u^5-677u^4v+529u^3v^2+2399u^2v^3+1088uv^4+114v^5)-$$ $$-4\left(u^2-5uv+v^2\right)^2\cdot288(u+v)\geq35586\sqrt{u^5v^5},$$ $$4(438u^6-2978u^5v+107u^4v^2+13656u^3v^3+20467u^2v^4+5822uv^5+438v^6)-$$ $$-4\left(u^2-5uv+v^2\right)^2\cdot4(31u^2+77uv+31v^2)\geq-6165u^3v^3,$$ $$4(42u^7-269u^6v-191u^5v^2+2403u^4v^3+5523u^3v^4+5249u^2v^5+851uv^6+42v^7)-$$ $$-4\left(u^2-5uv+v^2\right)^2\cdot(28u^3+82u^2v+82uv^2+28v^3)\geq11491\sqrt{u^7v^7}$$ and $$-3u^8+96u^7v-250u^6v^2+1288u^5v^3+1671u^4v^4+3368u^3v^5+1990u^2v^6+96uv^7-3v^8-$$ $$-4\left(u^2-5uv+v^2\right)^2(-u^4+16u^3v-7u^2v^2+16uv^3-v^4)\geq5432u^4v^4.$$ Now, let $a=\sqrt{uv}t.$
Thus, it's enough to prove that: $$19008t^6+80899t^5+99373t^4+35586t^3-6165t^2+11491t+5432\geq0,$$ which is obvious.
- 203,855
-
@Albus Dumbledore $\sum\limits_{cyc}(a^2+5b^2)(b^2+5c^2)=\sum\limits_{cyc}(a^2b^2+5a^2b^2+5a^4+25a^2b^2)=\sum\limits_{cyc}(5a^4+31a^2b^2).$ I hope now it's clear. – Michael Rozenberg Oct 07 '20 at 11:42
-
Though I have not checked, maybe assuming constraints due to homogeneity work to some extent? – Book Of Flames Oct 07 '20 at 13:08
-
-
I know that this in a way stupid: But how did you invent it without having the proof of this inequality? – Book Of Flames Oct 07 '20 at 16:54
-
@Book Of Flames I proved it, but by very ugly way and with helping of WA. Try to prove $\sum\limits_{cyc}(5a^4+31a^2b^2)+2\sqrt{\frac{1}{3}\prod\limits_{cyc}(a^2+5b^2)\sum\limits_{cyc}(28a^2+26ab)}\geq4(a+b+c)^4.$ I think it's very perspective. – Michael Rozenberg Oct 07 '20 at 17:15
-
1@MichaelRozenberg It is ingenious to introduce $\cdots \geq4\left(u^2-5uv+v^2\right)^2\cdots$. (+1) – River Li Oct 14 '20 at 00:38
-
@River Li Thank you! But this idea does not help for the following inequality. https://math.stackexchange.com/questions/1857856 – Michael Rozenberg Oct 14 '20 at 08:31
Probably not the proof you are looking for, but a proof nonetheless.
The inequality is really sharp, and I don't think that a manual solution exists. Concretely, I don't think that one can find a lower bound on the LHS, such that we can algebraically confirm that it upper bounds the RHS. However, it is easy to numerically verify that the inequality holds, and I hope that you can find this convincing.
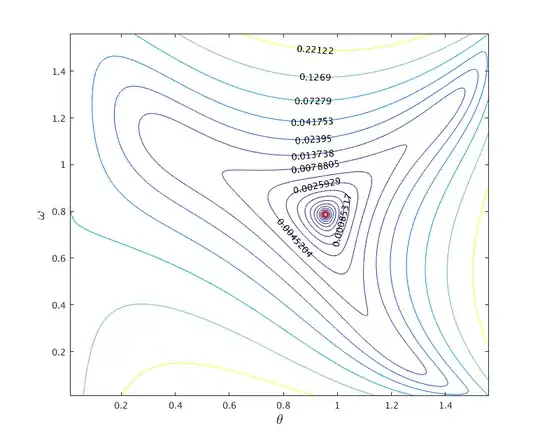
Specifically, divide both sides by $\sqrt{a^2 + b^2 + c^2}$, then we're left with the equivalent inequality: $$ \sqrt{x^2 + 5y^2} + \sqrt{y^2 + 5z^2} + \sqrt{z^2 + 5x^2} \geq \sqrt{10 + 8(xy + yz + xz)}, $$ where $x = \frac{a}{\sqrt{a^2 + b^2 + c^2}}, y = \frac{b}{\sqrt{a^2 + b^2 + c^2}}, z = \frac{c}{\sqrt{a^2 + b^2 + c^2}}$, and $x^2 + y^2 + z^2 = 1$. Furthermore, it has been established that we can safely assume that $x,y,z\geq 0$, so it is sufficient to verify the inequality on the surface $\{(x,y,z) \in\mathbb{R}^3 ~\vert~ x^2 + y^2 + z^2 = 1, x,y,z\geq 0\}$, which can be parameterized with $$x = \sin\theta\sin\omega,\quad y = \sin\theta\cos\omega,\quad z=\cos\theta,$$ with $(\theta,\omega)\in[0,\pi/2]\times[0,\pi/2]$.
Now, if one minimizes the function $$ h(\theta,\omega) = \sqrt{x^2 + 5y^2} + \sqrt{y^2 + 5z^2} + \sqrt{z^2 + 5x^2} - \sqrt{10 + 8(xy + yz + xz)}, $$ over the square $[0,\pi/2]\times[0,\pi/2]$, one then finds that it has a unique global minimum 0 at $x=y=z=\frac{1}{\sqrt{3}}$, or at $\theta \approx 0.9554,~ \omega = \pi/4$, see the figure below which shows the level sets of $h$.
This implies by homogeneity that the original inequality is equality only at $a=b=c$, and a strict inequality at all other values.
- 2,889
- 1
- 11
- 23
-
1How do you prove the unique minimization of $h(\theta,\omega)$ at the point you claim? The proof is not complete. – Hans Feb 20 '21 at 22:57
Here is a sketch of proof :
We show the hardest case when $a\geq b\geq c $ and $5a^2+c^2\geq 5b^2+a^2\geq 5c^2+b^2$
If we show the following statement :
Let $a\geq b\geq c>0 $ and $5a^2+c^2\geq 5b^2+a^2\geq 5c^2+b^2$ and $n\geq 400$ a natural number then we have :
$$\frac{1}{n+1}(5a^2+c^2)+\frac{n}{n+1}\Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big)\geq \frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\quad(1)$$
And :
$$\Big(\frac{1}{n+1}(5a^2+c^2)+\frac{n}{n+1}\Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big)\Big)\Big(\frac{1}{n+1}(5b^2+a^2)+\frac{n}{n+1}\Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big)\Big)\geq \Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big)^2\quad(2)$$
And :
$$\Big(\frac{1}{n+1}(5c^2+b^2)+\frac{n}{n+1}\Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big)\Big)\Big(\frac{1}{n+1}(5a^2+c^2)+\frac{n}{n+1}\Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big)\Big)\Big(\frac{1}{n+1}(5b^2+a^2)+\frac{n}{n+1}\Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big)\Big)\geq \Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big)^3\quad(3)$$
And then applying Karamata's inequality we show :
$$ \sqrt{\frac{1}{n+1}(5a^2+c^2)+\frac{n}{n+1}\Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big)\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}}+\sqrt{\frac{1}{n+1}(5b^2+a^2)+\frac{n}{n+1}\Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big) \frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}}+\sqrt{\frac{1}{n+1}(5c^2+b^2)+\frac{n}{n+1}\Big(\frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}\Big) \frac{10(a^2+b^2+c^2)-8(ab+bc+ca)}{9}}\geqslant\sqrt{10(a^2+b^2+c^2)+8(ab+ac+bc)} \quad(4)$$
Remains to apply this kind of inequality :
$$\sqrt{x}\frac{1}{k+1}+\sqrt{y}\frac{k}{k+1}\geq \sqrt{x\frac{1}{n+1}+y\frac{n}{n+1}}\quad (5)$$
Where $x,y>0$ and $n,k>0$ naturals numbers .
Applying $(4)$ to $(5)$ we get the desired inequality .
$(1)$ is trivial we prove $(2)$ now :
Due to homogeneity we put $a=1+p+q$ , $b=1+p$, $c=1$ and now we use WA .
See here for the LHS and here for the RHS of $(2)$ . If we substract each coefficient the remainders is positive wich prove the inequality $(2)$ .We can show $(3)$ by a similar way .
Hope you learn something from me and it helps you .
Regards Max
- 3,879
-
3Say please, how your post helps to prove the starting inequality? – Michael Rozenberg Oct 09 '20 at 20:47
-
-
-
@RiverLi it's partial but it works for some others values . Thanks to checks it ! I keep this in mind . – Barackouda Oct 10 '20 at 15:14
-
@ErikSatie So you need to make more assumptions besides $a\geq b\geq c$ and $\frac{a}{c}\geq\frac{b}{a}\geq \frac{c}{b}$ and $b\geq a\frac{(b+c)}{(a+b)}$. – River Li Oct 10 '20 at 15:20
-
@RiverLi can you confirm there is no mistakes in the last inequality that I cannot prove ?Thanks !! – Barackouda Oct 11 '20 at 11:57
-
-
-
@ErikSatie $\sqrt{5(a+c)^2+(b+c)^2}+\sqrt{a^2+5b^2}\geq \sqrt{10(a^2+b^2+c^2)+8(ab+bc+ca)}$ does not hold, given that $a \ge c \ge b > 0$, $a/b \ge c/a \ge b/c$. For example, $a=3472, b = 3056, c = 3471$. – River Li Oct 11 '20 at 13:17
-
@RiverLi look better my answer because if we have $b=x$ , $c=x+y$ , $a=x+y+z$ I add the condition $x\leq z$ or $b+c\leq a$ – Barackouda Oct 12 '20 at 08:15
-
@ErikSatie Can you give the complete condition for your partial answer in the first line of your answer? – River Li Oct 12 '20 at 10:36
-
-
2@ErikSatie I think that you should improve your writing which is not good for me to read. – River Li Oct 12 '20 at 11:15
-
-
@ErikSatie I think that it is not good to add constraints in the proof (for example, "Wich is true because we add the constraints" ). You should put complete constraints in the statement then you prove the statement. By the way, why you begin with initial capitals, for example, "Wich is true because we add the constraints :" should it be "which is true..."? – River Li Oct 12 '20 at 13:59
-
@RiverLi no problem I have not the time now but I shall correct it .Thanks!! – Barackouda Oct 12 '20 at 14:04
-
-
@RiverLi I admit that I cannot prove it without a computer and Karamata's inequality . Sorry for the waste of time .Regards Max. – Barackouda Oct 12 '20 at 17:17
-
@ErikSatie It is nice to discuss inequalities with you. This inequality is not easy by hand. – River Li Oct 12 '20 at 23:53
 $h(\theta,\omega)$" />
$h(\theta,\omega)$" />
from which we can obtain some bounds. I used it for $k=3$ inequality.
– River Li Oct 08 '20 at 15:51