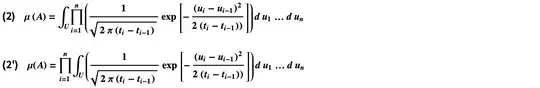Possible to prove - by induction or in any possible way - that Brownian motion increments are independent (starting from $(2)$)?

Question

I quote Kuo (2006):

Let $C$ be the Banach space of real-valued continuous functions $\omega$ on $[0,1]$ with $\omega(0)=0$.
A cylindrical subset $A$ of $C$ is a set of the form $$A=\{\omega\in C: (\omega(t_1),\omega(t_2),\ldots,\omega(t_n))\in U\}\tag{1}$$ where $0<t_1<t_2<\ldots<t_n\leq 1$ and $U\in\mathcal{B}(\mathbb{R}^n)$, the Borel $\sigma$-field.
Let $\mathcal{R}$ be the collection of all cylindrical subsets of $C$. Obviously, $\mathcal{R}$ is a field. However, it is not a $\sigma$-field.
Suppose $A\in\mathcal{R}$ is given by $(1)$. Define $\mu(A)$ by $$\mu(A)=\displaystyle{\int_U \prod_{i=1}^n}\bigg(\frac{1}{\sqrt{2\pi(t_i-t_{i-1})}}\exp\bigg[-\frac{(u_i-u_{i-1})^2}{2(t_i-t_{i-1}))}\bigg]\bigg)du_1\ldots du_n\tag{2}$$ where $t_0=u_0=0$

Theorem: The stochastic process $B(t,\omega)=\omega(t), 0\leq t\leq 1, \omega\in C,\text{ }$ is a Brownian motion

Well, as the above theorem, I am struggling to show independence of increments, in the mutual sense, not just pairwise (as required by definition), namely that $$B(t_1), B(t_2)-B(t_1),\ldots, B(t_n)-B(t_{n-1})\text{ are independent}$$ And this would be true if one showed that: $$\begin{split}\mu\{B(t_1)\leq a_1, B(t_2)-B(t_1)\leq a_2,\ldots, B(t_i)-B(t_{i-1})\leq a_i\}=\\=\mu\{B(t_1)\leq a_1\}\mu\{B(t_2)-B(t_1)\leq a_2\}\cdots\mu\{B(t_i)-B(t_{i-1})\leq a_i\}\end{split}\tag{3}$$ for $i=\{1,\ldots,n\}$.

---

I was trying to show $(3)$ by induction.

$(3)$ clearly holds true for $n=1$. Suppose now it holds true for $i=(n-1)$, so I have to show that it holds true for $i=n$ as well. So, starting point is:
$$\begin{split}\mu\{B(t_1)\leq a_1, B(t_2)-B(t_1)\leq a_2,\ldots, B(t_{n-1})-B(t_{n-2})\leq a_{n-1}\}=\\=\mu\{B(t_1)\leq a_1\}\mu\{B(t_2)-B(t_1)\leq a_2\}\cdots\mu\{B(t_{n-1})-B(t_{n-2})\leq a_{n-1}\}\end{split}\tag{4}$$ and I have to get to: $$\begin{split}\mu\{B(t_1)\leq a_1, B(t_2)-B(t_1)\leq a_2,\ldots, B(t_{n})-B(t_{n-1})\leq a_{n}\}=\\=\mu\{B(t_1)\leq a_1\}\mu\{B(t_2)-B(t_1)\leq a_2\}\cdots\mu\{B(t_{n})-B(t_{n-1})\leq a_{n}\}\end{split}\tag{5}$$

---

---

Is there any good way to pass from $(4)$ to $(5)$ relying on definition $(2)$?

Answer 1

Fix $0=t_0 < t_1 < \ldots < t_n$.

Lemma: $(2)$ is equivalent to $$\mu((B_{t_1},\ldots,B_{t_n}) \in U) = \int_U p(x) \, dx$$ for $$p(x) := \frac{1}{\sqrt{2\pi}^n} \frac{1}{\sqrt{\det C}} \exp \left(- \frac{1}{2} \langle x, C^{-1} x \rangle \right),$$ where $C \in \mathbb{R}^{n \times n}$ is defined by $c_{ij} := \min\{t_i,t_j\}$, $i,j=1,\ldots,n$ and $\langle x,y \rangle = \sum_{i=1}^n x_iy_i$ is the scalar product in $\mathbb{R}^n$.

Note that the result tells us that $(B_{t_1},\ldots,B_{t_n})$ is Gaussian with mean vector $m=(0,\ldots,0) \in \mathbb{R}^n$ and covariance matrix $C=(\min\{t_i,t_j\})_{i,j}$. This is not at all surprising: If $(B_t)_{t \geq 0}$ is indeed a Brownian motion, then this is exactly how the finite-dimensional distributions should look like.

Proof of the lemma: Denote by $M \in \mathbb{R}^{n \times n}$ the lower triangular matrix with entries $1$ on and below the diagonal. Denote by $D \in \mathbb{R}^{n \times n}$ the diagonal matrix with entries $d_i = t_i-t_{i-1}$ on the diagonal. Since $M^{-1}$ is a two-band matrix with $+1$ on the diagonal and $-1$ on the first sub-diagonal (below the diagonal), we can write

\begin{align*} \sum_{j=1}^n \frac{(x_j-x_{j-1})^2}{t_j-t_{j-1}}= \langle M^{-1} x, D^{-1} M^{-1} x \rangle &= \langle x, (M^{-1})^T \cdot (D^{-1} M^{-1} x) \rangle \\ &= \langle x, C^{-1} x \rangle \end{align*} for $C:=M D M^T$. (Note that $(M^{-1})^T = (M^T)^{-1}$.) Performing the matrix-multiplication of the above-defined matrices, we see that $C=(\min\{t_i,t_j\})_{i,j}$. As $\det(M)=1$, it also follows that $$\det(C) = \det(D) = \prod_{j=1}^n (t_j-t_{j-1}).$$ Plugging this into $(2)$, proves the lemma.

Note that, by the definition of $M$, we can write $$\Gamma:=\begin{pmatrix} B_{t_1} \\ \vdots \\ B_{t_n} \end{pmatrix} = M \cdot \Delta$$ where $\Delta := (B_{t_1}-B_{t_0},\ldots,B_{t_n}-B_{t_{n-1}})$. Equivalently, $$\Delta = M^{-1} \Gamma.$$ Since we know from our lemma that $\Gamma=(B_{t_1},\ldots,B_{t_n})$ is Gaussian, it follows that $\Delta$ is Gaussian as a linear combination of Gaussian random variables; more precisely,

\begin{align*} \mathbb{E}\exp(i \langle \xi, \Delta \rangle) = \mathbb{E}\exp(i \langle \xi, M^{-1} \Gamma \rangle) &= \mathbb{E}\exp(i \langle (M^{-1})^T \xi, \Gamma \rangle) \\ &= \exp(- \frac{1}{2} \langle (M^{-1})^T \xi, C (M^{-1})^T \xi \rangle) \\ &= \exp (-\frac{1}{2} \langle \xi, M^{-1} C (M^{-1})^T \xi \rangle ) \\ &=\exp(- \frac{1}{2} \langle \xi, D \xi \rangle), \end{align*} where we used in the last step that $C = MDM^T$ (see the proof of the lemma). This shows that the random vector $\Delta=(B_{t_1}-B_{t_0},\ldots,B_{t_n}-B_{t_{n-1}})$ is Gaussian with mean vector $0$ and covariance matrix $D$. Since $D$ is a diagonal matrix, this means, in particular, that $B_{t_1}-B_{t_0},\ldots,B_{t_n}-B_{t_{n-1}}$ are independent.

Answer 2

This nomenclature is more or less abstracted to get a mathematical foundation that is as broad as possible. Possibly it is a partition of the time interval (0,1] with finite many internally open intervals. So this finite set might cause still problems.

There no trick since the condition are picked by hand and as dubious as the abstraction of the cylindrical. It is assumed that this cylindricality is due to time - space considerations.

The method requires to deal with bilinear forms that are in general elliptic or hyperbolic. These bilinear forms are the arguments of the exponential function. We need for the step, not induction. That is subject to the randomness of the Brownian experiment. n is the small canonical size of the considered ensemble of the measured number of random steps the observed particle takes during the random experiment.

For sure if another step is observed this should be as independent from the others as all the steps before.

So what to do is state that the bilinear has the affinity zero it is not translated despite we consider translational motion and rotational motion together in the Brownian experiment. So all that has to be applied is a rotation of the coordinates of the bilinear form. Some prefer to name this transform to relative coordinates which too removes the affinity. v(i)=u(i)-u(i-1) for all i=1,..,n.

In this coordinates the integral factors and the integration can be exchanged with the product.

With this change the formulas (3)-(5) are valid. I think the given is notation has to be altered.

We can now make this transformation on the factors integrals back to the u(i)'s and have the representation.

Whether one prefers to name this a rotation of bilinear forms or transformation to relative coordinates between the positions the particle takes during the experiment. The basis to be allowed to do this is not the mathematical methodology of bilinear forms or relative coordinates but the independence of the theorem.

Theorem: The stochastic process (,)=(),0≤≤1,∈, is a Brownian motion.

The stochasticity grants the independence of the (,). The theorem is not the definition of stochastic processes nor is this the deep enough definition for Brownian motion. The formula (2) is needed in the theorem most. The individual function factors are normed and functions all with the domain ℝ->(0,1] and many more details. This is a probability distribution and so one. With goodwill, this is hidden or abstracted in the term stochastic process.

The requirement Borel -field demands the Banach space for abstraction or generalization. The Brownian motion is more restricted than this but there is no other theoretical framework available to express this foundation.

This induction step uses probabilities that are elsewhere used to measure biases of processes. That is not required for Brownian motions. All that is needed is the independence of the two steps. The outcome of step n does not influence the outcome of step n+1.

This is a mixture of neat mathematical thinking and experimental accessibility. The relative coordinates have most often to be calculated while the absolute position can and have to be measured. It is not a recipe for how to measure these positions.

Answer 3

Everything boils down to joint behaviour of Brownian motion at two certain times.

Let $0\le s < t$ and look at $(B(s),B(t))$. By $(2)$ we have that joint density of that vector is given by formula:

$$ g_{s,t}(x,y) = \frac{1}{\sqrt{2\pi s}}\exp(-\frac{x^2}{2s})\frac{1}{\sqrt{2\pi (t-s)}}\exp(-\frac{(y-x)^2}{2(t-s)}) $$

We are especially interested in $Cov(B(s),B(t)) = \mathbb E[B(s)B(t)]$ (the term $\mathbb E[B(s)]\mathbb E[B(t)]$ is zero, again due to $(2)$ (Indeed, using $(2)$ with only one time, that is for some $B(r)$ we get that $B(r) \sim \mathcal N(0,r)$)

We need to calculate it. Using Fubinii (due to integrability)

$$ \mathbb E[B(s)B(t)] = \int_{\mathbb R} \frac{x}{\sqrt{2\pi s}} \exp(-\frac{x^2}{2s}) \int_{\mathbb R} y \frac{1}{\sqrt{2\pi (t-s)}}\exp(-\frac{(y-x)^2}{2(t-s)}) dy dx $$

The inner integral is just the $\mathbb E[Z]$, where $Z \sim \mathcal N(x,t-s)$, so it's just $x$, hence: $$ \mathbb E[B(s)B(t)] = \int_{\mathbb R} \frac{x^2}{\sqrt{2\pi s}} \exp(-\frac{x^2}{2s}) dx $$

Similarly, this time we recognize something, too. It's $\mathbb E[Y^2]$, where $Y \sim \mathcal N(0,s)$, hence it's just $s$, and ... we're done.

We showed for any $0 \le s < t < 1$ that $Cov(B(s),B(t)) = s$. Clearly for $t=s$ it holds, too, since $B(r) \sim \mathcal N(0,r)$ as we said above. By symetry of Covariance, we showed that for any $s,t \in [0,1]$ we have $Cov(B(s),B(t)) = \min\{s,t\}$.

Now, we're ready to proceed. Take any $0=t_0 < t_1 < ... < t_n \le 1$. We want to show that $\{B(t_k)-B(t_{k-1}) : k \in \{1,...,n\} \}$ is an independent family. Note that vector $(B(t_1)-B(t_0),...,B(t_n)-B(t_{n-1}))$ is gaussian as a linear transformation of vector $(B(t_0),...,B(t_n))$ which is gaussian (due to assumption $(2)$ we have it's density). Hence it would be enough to show that covariance matrix is diagonal, hence it is enough to show that for $j \neq k$ (WLOG due to symetry assume that $j < k$) we have: $Cov(B(t_j)-B(t_{j-1}),B(t_k)-B(t_{k-1}))=0$. Indeed due to linearity:

$$ Cov( B(t_j) - B(t_{j-1}),B(t_k)-B(t_{k-1})) = Cov(B(t_j),B(t_k)) - Cov(B(t_j),B(t_{k-1})) - Cov(B(t_{j-1}),B(t_k)) + Cov(B(t_{j-1}),B(t_{k-1}))$$

Using $j<k$ so that $j \le k-1$, too and our result above, we get:

$$ Cov( B(t_j) - B(t_{j-1}),B(t_k)-B(t_{k-1})) = t_j - t_j - t_{j-1} + t_{j-1} = 0$$

Moreover (not needed in fact)

$$ Var((B(t_k) - B(t_{k-1})) = Var(B(t_k)) + Var(B(t_{k-1}) - 2Cov(B(t_k), B(t_{k-1})) = t_k + t_{k-1} - 2 t_{k-1} = t_k - t_{k-1} $$

So that the covariance of our Gaussian vector $(B(t_1)-B(t_0),...,B(t_n)-B(t_{n-1}))$ is given by $n \times n$ matrix:

$$ \begin{bmatrix} t_1 & 0 & 0 & ... & 0 \\ 0 & t_2-t_1 & 0 & ... & 0 \\ . & . & . & ... & . \\ . & . & . & ... & . \\ . & . & . & ... & . \\ 0 & 0 & 0 & ... & t_n-t_{n-1} \\ \end{bmatrix} $$

Hence our family is indeed independent (because measure of Gaussian vector with mean vector $(0,0,...,0)$ (our vector has such mean) and a diagonal covariance matrix is a product measure of $n$ real measures $\mu_1,...,\mu_n$, where $\mu_k \sim B(t_k)-B(t_{k-1}) \sim \mathcal N(0,t_k - t_{k-1}))$