I am studying the following problem. I want to obtain all the local minima of $$ \min_{x\in D} x^Tx \quad \quad \quad \quad \quad \quad (P.1) $$ where $x\in\mathbb{R}^n$ and $D = \{x: x^TA_ix = 1, \forall i=1,\dots,m\}$ and $A_1,\dots,A_m$ are a collection of $m<n$ positive definite $n\times n$ matrices. According to the Lagrange multiplier theorem ("Nonlinear programing" by Dimitry Bertsekas):
Proposition 3.1.1 (Lagrange Multiplier Theorem - Necesary Conditions) Let $x^*$ be a local minimum of $f$ subject to $h(x)=(h_1(x),\dots,h_m(x))=0$ and assume that the gradients $\nabla h_1(x^*),\dots,\nabla h_m(x^*)$ are linearly independent. Then, there exists a unique vector $\lambda^*=(\lambda_1^*,\dots,\lambda_m^*)$ called Lagrange multiplier vector such that $$ \nabla f(x^*) + \sum_{i=1}^m\lambda_i^*\nabla h_i(x^*) =0 \quad \quad \quad \quad \quad \quad (3.3) $$
Thus, the set of ALL local minima can be divided in two, the ones which have $\{\nabla h_i\}_{i=1}^m$ linearly independent (regular points), and such points may be found using (3.3), and other minima which have $\{\nabla h_i\}_{i=1}^m$ linearly dependent (nonregular points).
My question is: I already know how to find the regular points. My interest is regarding the nonregular ones. Can those nonregular points be studied (obtained) in my case? For reference, note that $h_i(x) = x^TA_ix-1$ and $\nabla{h_i}(x) = 2A_ix$.
From this point, let me explain what I have found up to now:
Suppose $\hat{x}$ is one of such points. I can partition the set of vectors $\mathcal{A}=\{A_i\hat{x}\}_{i=1}^m$ into two disjoint sets $\mathcal{B}=\{B_i\hat{x}\}_{i=1}^s\subset \mathcal{A}$ and $\mathcal{C}=\{C_i\hat{x}\}_{i=1}^r\subset \mathcal{A}$ with $r+s=m$ such that the vector in $\mathcal{B}$ are linearly independent and the ones in $\mathcal{C}$ are a linear combination of the ones in $\mathcal{B}$.
Then, there exists real constants $\{\alpha_{ij}\}_{j=1}^m$ such that $$ C_i\hat{x} = \sum_{j=1}^s \alpha_{ij}B_j\hat{x} $$ And for this point to lie in $D$ I require that $\hat{x}^TC_i\hat{x} = 1$ but also $\hat{x}^TB_j\hat{x}, j=1\dots,s$. Hence, it must be the case that $\sum_{j=1}^s \alpha_{ij}=1$ for $i=1,\dots,r$ and $j=1,\dots,s$. (is this useful?).
My original intention was to cast this as another (reduced) nonlinear program in which the gradients $\{\nabla h_i\}$ are linearly independent. My attempt was to try to show that $\hat{x}$ will be a local minimum of $(P.1)$ ignoring the "linearly dependent components". This is, if I solve (P.1) for all combinations of $\{A_i\}_{i=1}^m$, for example building $D$ only with the $A_i$ for separate, then by pairs, etc... then $\hat{x}$ would show up as a solution of one of those, in which the corresponding $\{\nabla h_i\}$ are linearly dependent. Is this true? The more I think about it the more I convince myself it is not the case. But what do you think? As an example of what I mean here, is the following. Consider $m=2$, $n=3$ and $A_1 = \text{diag}(1,1,0.1)$, $A_2 = \text{diag}(1,1,0.5)$. The constraints $x^TA_1x=1$, $x^TA_2x=1$ look like the red and blue surfaces here:
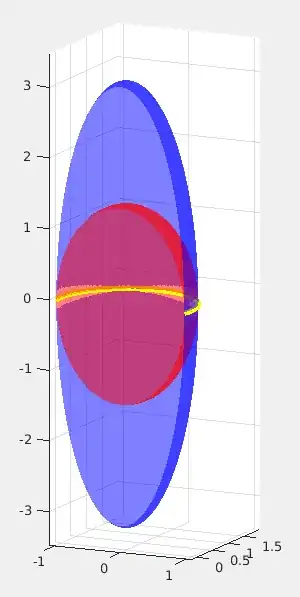
Their intersection is the yellow circle. Note that points in such intersection will have linearly dependent gradients, basically since $A_1x=A_2x$ for $x$ in such interection. However, if I study (P.1) just by taking into account $A_1$, I could still find those points. Of course this is just an example that motivated my idea, but It seems not to generalize.
My other attempt was to try to find explicitly all points that have $\{A_i\hat{x}\}_{i=1}^m$ linearly dependent. This is, find coeficients $\alpha_1,\dots,\alpha_m$ such that the matrix $H(\alpha)=\sum_{i=1}^m\alpha_iA_i$ is singular, and then look for $\hat{x}$ in the kernel of $H(\alpha)$ and see if such set of points intersect the problem constraints, etc... However, I haven't been able to obtain anything new from here.
What do you suggest me to do next? Do you think is possible to obtain such points? Actually any suggestion, advice, comment would be helpful for me.