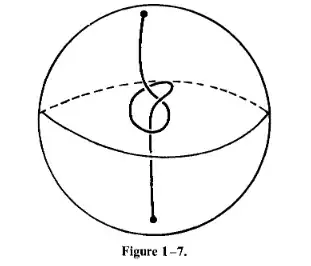
This problem comes at the end of Hirsch's $\textit{Differential Topology}$ (pg 32 #6). The picture is the following:
$K$ is the knotted string. The problem asks you to show there exists a smooth map $f:D^{3}\rightarrow D^{2}$ such that $K$ is the preimage of 0 which is a regular value. I've solved the problem two different ways. The first is thinking about $K$ as the trefoil in $S^{3}$ (glue on a ball to the exterior and connect the two end points). Now as a map from $\mathbb{C}^{2}\rightarrow \mathbb{C}$, and restricting to $|z|^{2}+|w|^{2}=1$, the map $f(z,w)=z^{2}+w^{3}$ has all the properties I want.
The second was is by resolving a crossing of $K$ by doing $\pm 1$ surgery to an unknot in $D^{3}$. The resulting manifold is diffeomorphic to $D^{3}$. All that to say there is a diffeomorphism $\phi:(D^{3},K)\rightarrow (D^{3},K')$ where $K'$ is the part of the z-axis contain in the ball. Now projection onto the $\pi:(D^{3},K')\rightarrow D^{2}$ given by projecting onto the x,y plane solves the problem since $\pi\circ \phi$ is a smooth map with all the desired properties.
My question: is there a more elementary way to solve this? I also tried the following but couldn't convince myself $K$ was the only thing in the preimage of 0 (or the 0 was a regular value): Let $f:K\rightarrow D^{2}$ such that $f(x)=0$ for all $x\in K$. Now since $K$ is a submanifold, every point $x\in K$ has a neighborhood $W_p$ such that locally, $$K\cup W = \{(x_{1},x_{2},x_{3}: x_{3}=x_{2}=0\}$$ (for some coordinate chart on W). Thus we have that in this coordinate chart, there is a function $F_{p}:W\rightarrow \mathbb{R}^{2}$ such that $F\big|_{K}=f$. Thus $f$ is a smooth function from $K$ to $D^{2}$ (Since every point has a neighborhood such that $f$ can be extended to a smooth function). $K$ is closed so there exists a complete extension, i.e., there is an $F:D^{3}\rightarrow D^{2}$ such that $F\big|K = f$. The proof of this uses a partion of unity (See Lee's $\textit{Smooth Manifolds}$ 1st ed pg 56). Looking at the proof, one sees that in fact $dF_{x}$ is surjective for all $x\in K$ and $\text{ker}(dF) = T_{x}K$. However, dF is taken to be 0 outside of a closed set containing $K$. So in particular, 0 is not a regular value.
If you have a way to modify this elementary proof or a novel way to prove the result other than the two over powered approaches I gave before, I'd enjoy seeing them.