$\underline{\mathrm{Note}}$
Since we need to draw quite a few auxiliary lines and mark even more number of angles and points, our diagrams are going to get confusingly crowded. We draw all auxiliary lines as dotted lines, so that OP can easily differentiate between auxiliary lines and the lines mentioned in the question. The added points are denoted by red letters. The size of angles, which followed directly from the problem description are marked green. The measures of all derived angles are given in black, while the angles, which we are striving to determine, are shown in red.
$\underline{\mathrm{Step\space 1}}$
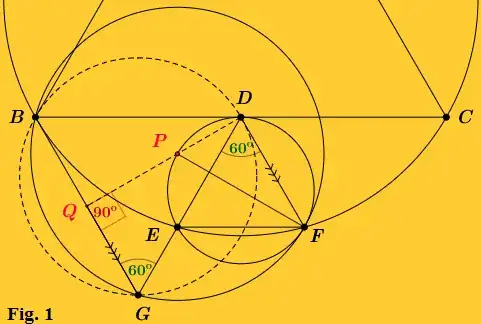
Consider $\mathrm{Fig.\space 1}$. As shown in this diagram, we have extended the OP’s sketch by drawing a line and the circumcircles of the equilateral triangle $BGD$. To be precise, a perpendicular has been dropped from the vertex $D$ of the triangle $BGD$ to opposite side $BG$ to meet it at $Q$. Since $BGD$ is an equilateral triangle, $DQ$ is the perpendicular bisector of $BG$. $DQ$ intersect the circumcircle of the triangle $DEF$ at $P$. Our aim is to prove that both the center of the circumcircle of $BGF$ and the point $H$, which is given as the diametrically opposite point of $F$ in OP’s sketch, lies on $DQ$.
Since $\measuredangle BGD = \measuredangle FDG$, the two lines $BG$ and $DF$ are parallel to each other. Therefore, the line $DQ$, which is perpendicular to $BG$, is perpendicular to $DF$ as well. This makes $\measuredangle FDQ$ a right angle and the circular arc $FDP$ a semicircle. Hence, $FP$ is a diameter of the circumcircle of the triangle $DEF$. However, it is given that $FH$ is a diameter of the same circle. Therefore, the two points $P$ and $H$ are one and the same. With this we have shown that $H$ lies on $DQ$, which is the perpendicular bisector of $BG$.
Furthermore, since $BG$ is the common chord of the circumcircles of the two equilateral triangles $BGF$ and $BGD$, their individual centers lies on $DQ$.
$\underline{\mathrm{Step\space 2}}$
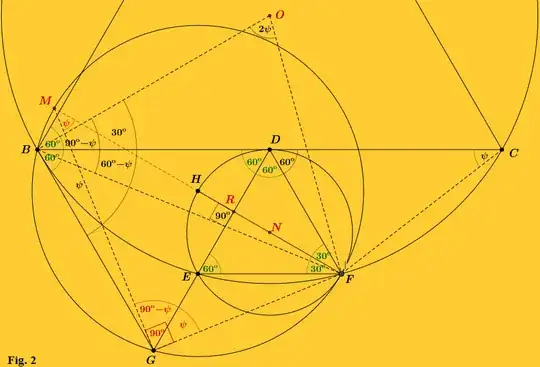
The source of $\mathrm{Fig.\space 2}$ is also the OP’s sketch. We extend the existing line $FH$ to meet the circumcircle of $BGF$ at $M$. We denote the intersection point between $FH$ and $DE$ as $R$. We add two more new points, $N$ and $O$, which are the circumcenters of the triangles $DEF$ and $ABC$ respectively. Let $\measuredangle FCD = \psi$. Our aim is to show that $FM$ is a diameter of the circumcircle of $BGF$.
The chord $BF$ of the circumcircle of $ABC$ subtends $\measuredangle FOB$ at the circumcenter of $ABC$, while subtending $\measuredangle FCB$ at its circumference. Therefore, $\measuredangle FOB = 2\measuredangle FCB = 2\psi$. Since its sides $FO$ and $OB$ are radii of the circumcircle of $ABC$, $FOB$ is an isosceles triangle. Therefore, we shall write, $\measuredangle OBF = 90^0-\psi$.
Now, pay your attention exclusively to the angles at point $B$. Since $OB$ is a radius of its circumcircle, it is also the angle bisector of vertex angle $B$ of $ABC$. Therefore, $\measuredangle OBC = 30^o$, and hence,
$$\measuredangle CBF = \measuredangle OBF- \measuredangle OBC = 90^o-\psi-30^o=60^o-\psi.$$
We keep on chasing angles to obtain,
$$\measuredangle FBG = \measuredangle CBG- \measuredangle CBF = 60^o – \left(60^o-\psi\right) = \psi.$$
Both $\measuredangle FMG$ and $\measuredangle FBG$ are subtended at the circumference of the circumcircle of $BGF$ by the same chord $GF$. Thus, we have,
$\measuredangle FMG = \measuredangle FBG = \psi.$
It is given that $FH$ is a diameter of the circumcircle of the triangle $DEF$, which makes $FH$ the perpendicular bisector of $DE$, the opposite side of its vertex $F$. This means that $\measuredangle GRM$ is a right angle. Now, we can determine the $\measuredangle MGR$ of the triangle $MGR$ as shown below.
$$\measuredangle MGR = 180^o - \left( \measuredangle GRM + \measuredangle FMG\right) = 180^o - \left(90^o+\psi\right) = 90^o - \psi$$
Let us now divert the focus of our investigation to the two triangles $DGF$ and $DFC$. They share a side, namely $DF$. Furthermore, their angles $FDG$ and $CDF$ are equal. Since $BD$ and $BG$ are two sides of the same equilateral triangle, namely $BGD$, $DG = BD$. $D$ is the midpoint of $BC$, hence, $CD = BD$. Therefore, $CD = DG$. According to $\mathit{Euclid I.4}$ (also known as SAS Theorem), these two triangles are congruent, which gives us $\measuredangle DGF = \measuredangle FCD = \psi$. Thus, we shall write,
$$\measuredangle MGF = \measuredangle MGR + \measuredangle DGF = 90^o - \psi + \psi = 90^o, $$
which indicates that $FM$ (or the extended $FH$) is indeed a diameter of the circumcircle of $BGF$.
$\underline{\mathrm{Conclusion}}$
In $\mathrm{Step\space 1}$, we showed that point $H$ and the circumcenter of $BGF$ lies on the perpendicular bisector of its side $BG$, namely $DQ$.
In $\mathrm{Step\space 2}$, we made it clear that $FM$, which actually is the extended $FH$, is a diameter of the circumcenter of $BGF$.
Now, the circumcenter of $BGF$ must lie on the intersection point of $DQ$ and $FM$. Since the point $H$ is common for both these lines, it is the sought circumcenter of $BFG$.
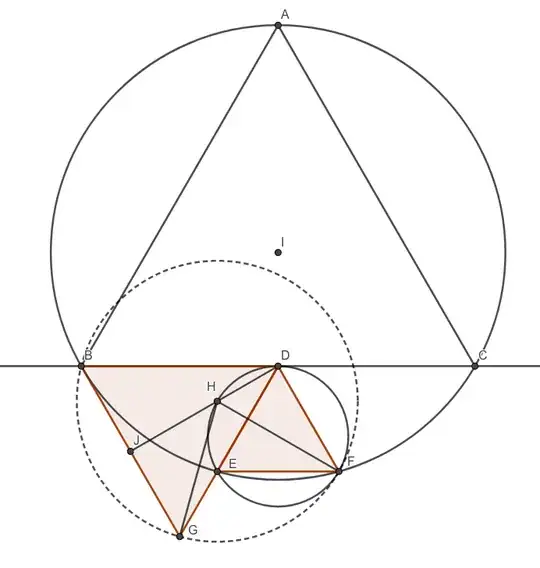
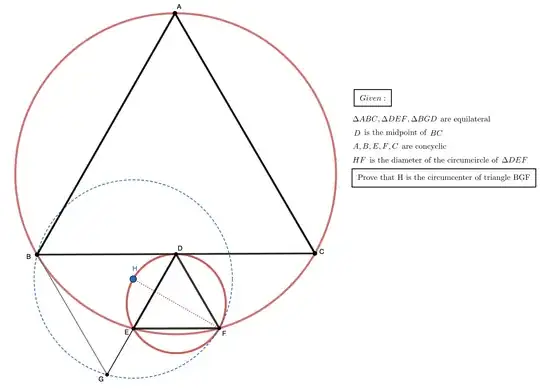 $$\Delta ABC \text{ is an equilateral triangle with } D \text{ being the midpoint of } BC \text{. } \Delta DEF \text{ is also an } \\ \text{equilateral triangle such that } E, F \text{ are on minor arc } BC \text{ of the circumcircle of } \Delta ABC \text{ with } \\ DE \parallel AB \text{ & } DF \parallel AC \text{. } \Delta BDG \text{ is equilateral } \text{such that } E \text{ lies on } DG\text{. } \text{ Let } H \text{ be the point on the } \\ \text{circumcircle of } \Delta DEF \text{ such that } HF \text{ is the diameter} \text{. Prove that } H \text{ is the circumcenter of } \Delta BGF.$$
$$\Delta ABC \text{ is an equilateral triangle with } D \text{ being the midpoint of } BC \text{. } \Delta DEF \text{ is also an } \\ \text{equilateral triangle such that } E, F \text{ are on minor arc } BC \text{ of the circumcircle of } \Delta ABC \text{ with } \\ DE \parallel AB \text{ & } DF \parallel AC \text{. } \Delta BDG \text{ is equilateral } \text{such that } E \text{ lies on } DG\text{. } \text{ Let } H \text{ be the point on the } \\ \text{circumcircle of } \Delta DEF \text{ such that } HF \text{ is the diameter} \text{. Prove that } H \text{ is the circumcenter of } \Delta BGF.$$