0

I have this contour, to help with evaluating $\int_{\gamma_\epsilon} \frac{e^{iz}-1}{z} dz $ over: pg1

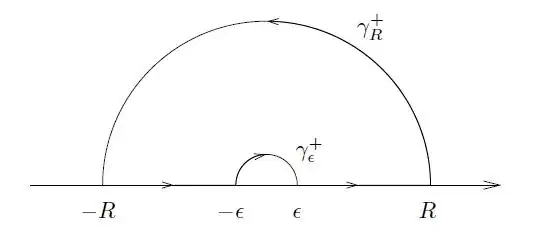
I have $\frac{e^{iz}-1}{x} \to\frac{iz}{z} \to i$.

I have trouble integrating: $\int_{\gamma_\epsilon} i dz$.I set $z=\epsilon e^{i\theta} dz = i \epsilon e^{i\theta}$,soI get : $\int_{0}^{\pi} i i \epsilon e^{i \theta} d\theta = 0$ as $\epsilon \to 0$, which I think is wrong.

What am I doing wrong?

u_any_45
  • 173

1 Answers1

1

Nothing wrong with your calculation. If $z=\epsilon e^{i\theta}$, then $dz=izd\theta$ and $dz/z=id\theta$ so the integral over the small contour $\gamma_\epsilon^+$ becomes:

$$\oint_{\gamma_\epsilon^+}\frac{e^{iz}-1}{z}dz=\oint_{\gamma_\epsilon^+}(e^{iz}-1)\frac{dz}{z}=\oint_{\gamma_\epsilon^+}(e^{iz}-1)id\theta$$

When $\epsilon\to 0$, $z\to 0$ and this reduces to:

$$\int_{\pi}^0 0\cdot id\theta=0\cdot i\int_\pi^0 d\theta=0$$

(For the upper semi-circle integral $\oint_{\gamma_R^+}$, try to bound the integrand through $R\to\infty$).

  • It should go to $-\pi$ @YiannisGalidakis. The outer circle goes to 0, as $R \to \infty$ – u_any_45 Sep 17 '20 at 14:57
  • @curious_analyst. What should go to $-\pi$? Yes, the upper semi-circle integral will go to 0. –  Sep 17 '20 at 15:04
  • The small semicircle with radius $\epsilon$,i.e. $\gamma_{\epsilon +} $ @YiannisGalidakis – u_any_45 Sep 17 '20 at 15:05
  • @curious_analyst Do you mind showing me what you have in mind? –  Sep 17 '20 at 15:08
  • This post (Answer 1) does a different method of calculating the integral of $\gamma_{\epsilon +}$. https://math.stackexchange.com/questions/1739621/the-infinite-integral-of-frac-sin-xx-using-complex-analysis – u_any_45 Sep 17 '20 at 15:15
  • @curious_analyst. That's right. But that's for a slightly different function. His integrand is $e^{iz}/z$. Yours is $(e^{iz}-1)/z$. The -1 kills the integrand as $z\to 0$. –  Sep 17 '20 at 15:19
  • Let us continue this discussion in chat. – u_any_45 Sep 17 '20 at 15:22
  • @curious_analyst Sorry, I am a bit busy at the moment for chat. If you find another way to invalidate the result (0), please post it here and I will look at it. Cheers. –  Sep 17 '20 at 15:29
  • Sure @YiannisGalidakis. I was trying to evaluate the same integral $\int_{0}^{\infty} \frac{sinx}{x} dx$. The equivalent complex integral I took was $\int \frac{e^{iz} -1}{z} dz$ hoping that the integral I want to evaluate to evaluate is $\frac{1}{2i}\int_{-\infty}^{\infty} \frac{e^{ix}-1}{x} dx$.He used a different equivalent complex integral. – u_any_45 Sep 17 '20 at 15:43
  • @curious_analyst: "He used a different equivalent complex integral...", Sorry, there's only one equivalent complex integral to the problem and that's the one he uses in his answer ($\exp(iz)/z$). Your integral is not equivalent and will not give you the correct result. But as far as it is concerned, your calculation for the contour of your integral ($(\exp(iz)-1)/z$) was correct. Sorry, my answer addressed YOUR calculation of YOUR integral, not whether your equivalent integral or method is correct or not. Try to see the difference, please. –  Sep 17 '20 at 15:57
  • This integral was the recommended integral in Stein and Shakarchi @YiannisGalidakis. – u_any_45 Sep 17 '20 at 16:36
  • 1
    @curious_analyst. It may have been, but the method is not equivalent. Does the author say HOW this integral gives results for the integral $\sin(x)/x$? In any case, note that the integral splits to two integrals as: $e^{iz}/z$ and $-1/z$, so if you carefully keep track of your overall integral, then yes, you'll get similar results, since there's a factor of $-2\pi i$ contributing from the $-1/z$ integral. But regardless, your calculations for THIS integral were correct, so what are we arguing about, really? –  Sep 17 '20 at 16:52