Is the line created by the minor axis of an ellipse concurrent to the lines running to the opposite vanishing point?

Question

My questions needs more context than what can fit into the title so let me elaborate. In pretty much all the art textbooks I am reading on linear perspective they state that the correct way of placing an ellipse is to imagine the minor axis of an ellipse as an axel of a wheel running to the opposite vanishing point. Here are examples for the various types of perspective the textbooks mention.

One point perspective:

In one point perspective only one set of parallel lines of a cuboid are concurrent, the other two sets are parallel (one set parallel to the horizon, the other perpendicular to it). If we plot an ellipses inside a one-point square the minor axis' should all run vertical (to the non-concurrent vanishing point). We find that only ellipses whose major axis are perpendicular to the vanishing point (A`) have this property.

Two point perspective:

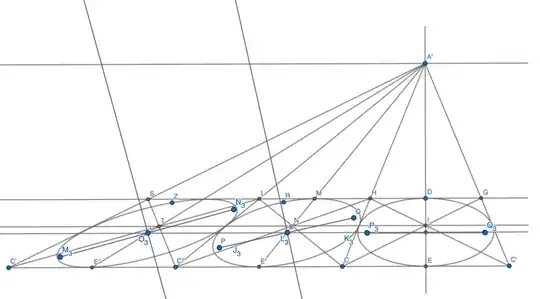
In two point perspective two of the sets of parallel lines of a cuboid are concurrent (meeting at R3 & S3 in the image) and the other set are not concurrent (parallel). I tried placing an ellipse such that the perspective center points of the sides of the quadrilateral are the tangent points of the ellipse but the minor axis does not seem concurrent with the lines running to the opposite concurrence (vanishing point). It should be stated that the two quadrilateral and their concurrences are a mirror reflection of each other, but this is not always the case in two point perspective.

If I adjust the size of the bounding quadrilateral I can make the minor axis concurrent with the lines running to the opposite vanishing point... but what if I want an ellipse placed inside a different sized quadrilateral?

Am I missing something in my plotting of ellipses or are the authors of these textbooks mistaken?

Answer 1

You are absolutely right; the authors of these textbooks are mistaken, and your diagrams show why.

I happen to have watched a fair number of instruction videos on perspective drawing, and to my frustration, I haven't yet found a single one that addresses this mistake, even from the most meticulous and formal instructors.

This is somewhat understandable. Broadly speaking, artists establish rules based on aesthetics, intuition, and approximation; whereas mathematicians remain skeptical without proof. These are two valid mindsets for two different fields, and your question belongs to the overlap of the two. The danger of an artist learning the technical craft of perspective is that they might use rules of thumb indiscriminately without fully understanding when they apply. The danger of a mathematician learning to draw is that they might break out a straightedge and compass without considering whether that will actually contribute to a successful composition. It would be nice to find a happy middle ground between these two camps, but ellipses turn out to be surprisingly complex. A perfect geometric construction exists, but just isn't worth it in the the context of a larger drawing, so it's natural to look for a simpler way.

Note that the rule actually does work for isometric drawings. In other words, if all parallel lines remain parallel (as opposed to converging to a vanishing point), then it holds. There are other cases where it holds, as you allude to in the comments. Most importantly, the rule will be reasonably close when the drawing is within the cone of vision. In contrast, in your first example, the leftmost circle is outside the cone of vision and therefore quite distorted.

In summary, the "rule" should be considered a good approximation most of the time, but the more distortion there is, the more likely you should abandon it and use your instincts (or a straightedge and compass).

Answer 2

Minor/major axes, foci, etc. are "metric objects" that have a meaning in the framework of metric geometry, therefore are outside the scope of projective geometry which (in particular) doesn't preserve neither the lengths nor the ratio of lengths (but the cross-ratio). As a consequence, it is not astonishing that you find such discrepancies...

Besides, are you aware of the fact that a figure like your first figure can be easily obtained by programmation in a convenient language. For example, this figure:

Fig. 1. Figure generated by a program written in Matlab (see bottom of this answer) The vanishing points are materialized by red dots. We see on this figure that we cannot infer anything on the orientations of the major/minor axis of the ellipses...

Here is another figure, similar to the first one you have given with trapezoids instead of general quadrilaterals:

Fig. 2: Figure obtained by changing $A$ into $[5+0.i,1+2i,0+0i]$ and changing denominator $(x+y+t)$ into $(y+t)$ in function $Z$. Only a single vanishing point at finite distance (the other one being at infinity).

Explanation: everything is based on the common (and simple) expression of all projective transformations (in particular those giving a perspective):

$$X=\dfrac{ax+by+c}{gx+hy+k}, \ \ Y=\dfrac{dx+ey+f}{gx+hy+k}, \tag{1}$$

(please note the common denominator) or equivalently:

$$Z=\dfrac{Ax+By+Ct}{gx+hy+kt}\tag{2}$$

$$\text{with} \ Z=X+iY, A=a+id, B=b+ie, C=c+if,$$

with $t=1$ for ordinary points and $t=0$ for points at infinity.

(using complex numbers for plane geometry is very handy).

Remark:

Here, in the plane with coordinates $(x,y)$, I have first described a chain of 6 tangent circles (+ circumscribed squares) to which I have applied a certain projective transform of the type given by (2).

Program:

clear all;close all;hold on
A=[2+i,1+1i,0+0i]; % could be (almost) any set of comp. numbers
Z=@(x,y,t)((A(1)*x+A(2)*y+A(3)*t)./(x+y+t)); % see formula (2)
s=5; % shift
a=0:0.01:2*pi; % parameter
for k=1:4;
   % ellipses as images of circles by "Z transform":
   plot(Z(cos(a)+2*k,sin(a)+s,1)); 
   % quadrilaterals as images of squares: 
   plot(Z([-1,1,1,-1,-1]+2*k,[-1,-1,1,1,-1]+s,1)); 
end;
% vanishing points in the 2 directions, with $t=0$:
plot(Z(1,0,0),'or','markerfacecolor','r'); 
plot(Z(0,1,0),'or','markerfacecolor','r');

Answer 3

Imagine a cylinder (prism with a circle as its base) rotated in space. I guess we all agree that the minor axes of the ellipses at the ends of that cylinder on the picture plane are parallel to the sides of the cylinder. Therefore they share a vanishing point. Now construct a rectangular prism such that the sides of the prism are tangent to the cylinders mantle surface. The base of this prism will be a square. The prism can arbitrarily be rotated around the axis of the cylinder but the tangent faces will still share the vanishing point with the cylinder and therefore with the minor axis of the ellipses created by the cylinder.

The art books on perspective drawing propably refer to either prisms with a square or a circle as their base. Therefore the above mentioned authors are correct for the implied boundary conditions.

Answer 4

I know it has been over three years and all but I am an art student who came across this post when I was trying to figure out the minor axis better for myself. I do think I can help clear up some of the confusion here based on some of the perspective theory that I do know of, and fill in some more gaps with deduction. Maybe it could still help someone else out there.

In short, Phillip Meyer (the person who posted an answer above mine, I believe) is correct. That's what they teach you in an actual perspective class.

For the longer version, here it goes:

In the first diagram, if we were to assume that you have three squares at an angle containing a circle each, then we can see that the minor axes converge to a VP far below the horizon. And that is consistent with the idea of a minor axis of a circle in perspective always converging to the vanishing point perpendicular to its plane. The confusion here arises because what you have in your first diagram are probably not circles, but ovals in perspective that also look like ellipses. I believe you can find resources that can show you how to make sure you have an accurate ellipse in perspective but I think that process is pretty long. Note that in a more ideal set up for One Point Perspective, you would just be looking at a circle straight on.

In your second diagram, the minor axis of the ellipse does not converge with the vanishing point of its bounding box. There are two potential reasons why this is happening.

1. IF this is a cylinder, and the ellipse that we see here is a circle in perspective, then you have made a perspective error. You need to either converge the lines of this bounding box to the vanishing point found by intersecting the minor axis and horizon, or you need to change the plane containing the ellipse such that its minor axis meets at the correct vanishing point.
2. IF this is not a cylinder, and it's an oval shape in perspective, then the minor axis rule is no longer applicable. I am guessing that the perpendicular axis for this ellipse is derived from connecting the VP (R3) to the perspective center of this oval (D3).

In your third and last diagram, you modify the bounding plane such that the minor axis meets the vanishing point, R3. This is how it would look if you were depicting a cylinder in perspective. Its minor axis would meet the vanishing point that's perpendicular to its plane.

Lastly, I saw in your response to Phillip Meyer that you believe you have projected a cylinder in perspective in your second diagram. This is incorrect because of what I mentioned earlier but it's a common mistake to make. Perspective Books really don't explain this sufficiently either. The confusion arises because both a circle and oval look like ellipses when projected in perspective. How would one know the difference when drawing them? Again, there might be someone out there with a precise method but for most drawing purposes, it's up to you to decide what you want it to be. If you want it to be a cylinder, simply make sure that when you draw out its body or bounding box etc., that you keep those lines parallel to the minor axis and converge them appropriately.

If you are wondering why this minor axis rule only applies to circles in perspective and not ovals, the answer lies in the symmetry of circles. The way I personally think about it is this: You take a circle and tilt it in one, two or even three axes, it will look like an ellipse. The points connected by the major axis experience the least foreshortening and the points connected by the minor axis experience the most amount of foreshortening. Generally it wouldn't be this simple to discern with any other shape including an oval, but since a circle is symmetrical and all the points on this circle are the same amount of distance away, you can pretty easily tell the direction in which the most amount of foreshortening is happening for any pair of diametrically opposite points. This gives you the direction of its depth or Z axis. And by definition, the two closest diametrically opposing points on an ellipse are connected by the minor axis.

For a real world example, think of a how a Ferris Wheel works. You can imagine the XY plane within which the cabins are moving along the circular path with its axle being the Z Axis. Seen from any other angle that's not directly facing it, or from the side, this circular path will look like an ellipse and that shape will not be disturbed by the movement of the cabins. Now imagine if that Ferris wheel was not a circle but an oval, and you're still viewing it from the same angle. Perhaps you can imagine that as the cabins move, it would be unable to maintain a constant shape like the circular ferris wheel. Different parts of that oval shape will get foreshortened differently with every bit of rotation even as its axel (Z axis) remains the same. So you can hopefully sense that the major and minor axes would no longer have that same relationship with the Z axis in this case.

I could be wrong about a lot of it too since I have just made up this hypothesis for myself because it confused me as well. Perspective books generally avoid this topic for some reason. I have personally not come across anything out there that would help me understand this any better but I'll keep trying to look out for better sources.