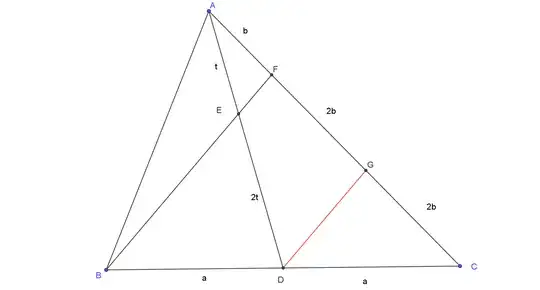
In the figure below, $AD$ is the median on $BC$. The point $E$ divides $A$ and $D$ in the ratio $1:2$. $BE$ produced meets $AC$ at $F$. Find the value of $AF:FC$
My try: I joined $E,C$.Let area of $\Delta ABC=x$ Then we get $$ar(BED):ar(ABE)=2:1$$ Also $$ar(ABD)=\frac{x}{2}$$ $\implies$ $$ar(BED)=\frac{2x}{6}$$ $$ar(AEB)=\frac{x}{6}$$ So $$ar(ECD)=\frac{2x}{6}$$ $\implies$ $$ar(AEC)=\frac{x}{6}$$ Any way from here?
Let $G$ halves $FC$, then $FG= GC = 2b$ and $DG||BF$ (by Thales theorem).
Then, again by Thales: $AF: FG = AE: ED = 1:2$ so $AF = b$ and thus $AF:FC = 1:4$
As per Menelaus's theorem applied to $\triangle ADC$ and line $BEF$:
$$\frac{\vec{AE}}{\vec{ED}}\times\frac{\vec{DB}}{\vec{BC}}\times\frac{\vec{CF}}{\vec{FA}}=-1$$
i.e. $$\frac{\vec{AF}}{\vec{FC}}=-\frac{\vec{AE}}{\vec{ED}}\times\frac{\vec{DB}}{\vec{BC}}=-\frac{1}{2}\times\left(-\frac{1}{2}\right)=\frac{1}{4}$$ i.e. $AF:FC=1:4$.
We use mass point geometry. Put masses $1kg, 1kg, 4kg$ at $B,C,A$ respectively. Clearly, $D$ is center of mass of $B$ and $C$ and $E$ is center of mass of $A$ and $D$ and thus, $E$ is center of mass of $(A,B,C)$. Hence, $F$ is center of mass of $A$ and $C\implies AF:FC=\text{mass$(C):$ mass$(A)$}=1:4$.
Let $\mathcal{H}_{X,k}$ denote a homothety with center at $X$ and a extension factor $k$.
We have a following fact (Theorem):
If $\mathcal{H}_{M,k_1}$ and $\mathcal{H}_{N,k_2}$ are homotheties then their compostion $\mathcal{H}_{M,k_1}\circ \mathcal{H}_{N,k_2}$ is again some homothety $\mathcal{H}_{S,k}$ with $k=k_1k_2$ (if $k\ne 1$) and it center $S$ lies on a line $MN$.
Since we have: \begin{align}\mathcal{H}_{B,{1\over 2}}: &\; C \longmapsto D\\ \mathcal{H}_{E, -{1\over 2}}: & \;D \longmapsto A\\ \end{align} we see that $F$ is a center of homothety which takes $C$ to $A$ with ratio $-{1\over 4}$, so $AF:FC = 1:4$.