I have been studying the Duffing oscillator rather intensively lately, mainly based on the theory in of the book by Guckenheimer and Holmes. From all that I have gathered, it seems that most dynamical systems show a period doubling cascade before going into chaos. For example, the logistic map and the driven damped pendulum show this behavior. For instance, this a bifurcation diagram for the pendulum:
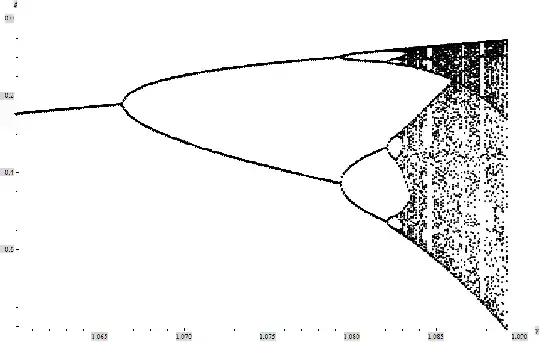
However, when I calculate numerical solutions of the Duffing oscillator with Mathematica, I am unable to find such a period doubling and the system goes into chaos right away, as this bifurcation diagram shows:

Now I have tweaked and played with parameters and initial values, calculated some parts in more detail, but whatever I try, I still cannot find any period doubling. I find this very puzzling, since apparently period doubling does take place for the Duffing oscillator, according to Guckenheimer and Holmes. Also, I thought that it was a universal phenomenon for chaotic systems. I could not come up with any reason why I fail to find it other than shortcomings of the numerical method of Mathematica I used (I simply used NDSolve and ParametricNDSolve). Could there be any other reason why a period doubling is absent?