Parabola through 4 points

Question

Three fixed points are given in the plane.

Along with the three given fixed points what is the equation of the parabola with variable fourth point $(x,y)$ and also what geometrical property of the parabola is altered by the variable point not in the red zone defined by Jean Marie?

Let me explain my question:

Three points define a circle of a unique circum-radius. Five points determine a conic of a unique eccentricity.

And by the same token what is the unique property of a parabola through four points?

I remember setting the discriminant to zero in standard form of general conic obtaining two parabolas $y=\pm \sqrt{ax+b}+(cx+d $) with 4 constants but could not readily get to an elegant form in terms of $(x1,y1),(x2,y2),(x3,y3)$, or if possible as a product of two factors.

Thanking you in advance.

Answer 1

This can be recasted into the so-called "Newton's problem" as treated in the classical book of H. Dörrie, "100 Great Problems of Elementary Mathematics" which can be found here (problem 45 page 208) where it is shown that a parabola (in fact two of them) can pass through 4 points.

In fact, we can give four equivalent conditions ($C_1) ... (C_4)$ for the fact that there exist a parabola through the 3 first points and the fourth point :

• ($C_1$): the 4 points form a convex quadrilateral.

As a consequence, let $T$ be the "filled" triangle formed by the three initial points.

• ($C_2$): [There is a parabola through the 3 first points and the fourth point] if and only if the fourth point is in the complementary set of the forbidden red region represented in the following figure (triangle $T$ + $3$ unbounded regions).

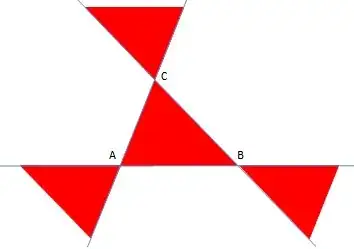
Fig. 1: Forbidden regions for the fourth point (in red)._

Remark : I am very indebted to Oscar Lanzi who has pointed an error of mine about condition $(C_2)$ in a previous formulation ; moreover, he has pointed the exceptional case where the points form a parallelogram: in this case, the parabola(s) are degenerated into 2 parallel lines.

• $(C_3)$: the barycentrical coordinates of the fourth point must have two positive and one negative component.

• $(C_4)$:

$$\dfrac{\begin{vmatrix}x_4&x_2&x_3\\ y_4&y_2&y_3\\1&1&1\end{vmatrix}\begin{vmatrix}x_1&x_4&x_3\\ y_1&y_4&y_3\\ 1&1&1\end{vmatrix}\begin{vmatrix}x_1&x_2&x_4\\ y_1&y_2&y_4\\ 1&1&1\end{vmatrix}}{\begin{vmatrix}x_1&x_2&x_3\\ y_1&y_2&y_3\\ 1&1&1\end{vmatrix}^3}\color{red}{<0} \tag{1}$$

(Exponent 3 can be suppressed.)

(1) can be given the equivalent symmetric form:

$$\begin{vmatrix}x_1&x_2&x_3\\ y_1&y_2&y_3\\1&1&1\end{vmatrix}\begin{vmatrix}x_2&x_3&x_4\\ y_2&y_3&y_4\\ 1&1&1\end{vmatrix}\begin{vmatrix}x_3&x_4&x_1\\ y_3&y_4&y_1\\ 1&1&1\end{vmatrix}\begin{vmatrix}x_4&x_1&x_2\\ y_4&y_1&y_2\\ 1&1&1\end{vmatrix}\color{red}{>0}$$

The sign change comes from the fact that some pairs of columns were interchanged in order to obtain a global symmetric form.

Remark: M. Woltermann (Washington and Jefferson College) had undertook a huge task: providing a digital version of the above mentionned book "One Hundred great Problems of Mathematics" originaly published in german in 1932 by Heinrich Dörrie, meanwhile (intelligently) grooming it. But unfortunately, his site is no longer available.

A very detailed analysis of the Newton's problem can be found here.