2

I'm currently doing high school second year trigonometry but this is just something that came to my mind.

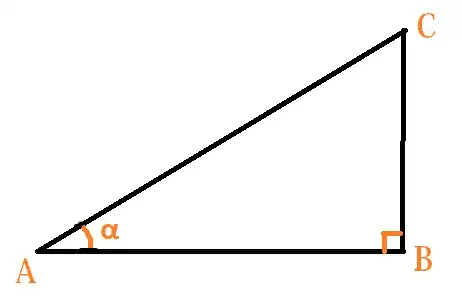
The figure below shows a right angled triangle $ABC$, where $\angle A = \alpha$, $\angle B = \dfrac{\pi}{2}$ or $90^\circ$.

Figure - 1

Now, in introductory trigonometry, the trigonometric functions of an angle are defined as ratios or sides of a right angled triangle. For example : $\sin\alpha = \dfrac{BC}{AC}$.

In the textbook I learned trigonometry from, this were the contents of the first few pages :

  • What is trigonometry?
  • It's applications in other fields of Mathematics and outside of Mathematics
  • Definition of trigonometric functions (or ratios)
  • Examples and questions

    The first example was as follows :

    You are provided with two triangles. Let those triangles be $XYZ$ and $PQR$. Both of these triangles are right angled triangles. $\angle Y = \angle Q = 90^\circ$. Also, $\angle X = \angle P$. Let these two angles be equal to $\varphi$. Now, $XZ = 5 \text{ units}$, $YZ = 3 \text{ units}$ and $PR = 10 \text{ units}$. Find $QR$.

    The solution was as follows : $$\sin\varphi = \dfrac{\text{Perpendicular}}{\text{Hypotenuse}} = \dfrac{3}{5} \text{, obtained from } \Delta XYZ$$ $$\text{From }\Delta PQR \text{, } \sin\varphi = \dfrac{QR}{10}$$ $$\therefore \sin\varphi ~ \dfrac{3}{5} = \dfrac{QR}{10} \implies QR = \dfrac{10 \cdot 3}{5} = 6 \text{ units}$$

    I think that prior to this,. the following statement should have been proved :

    The trigonometric ratios of an angle are unique and do not depend on the triangle chosen.

    I don't think think that this solution would be valid before proving that the sine of $\varphi$ obtained from both the triangles is unique. The statement that I have mentioned above can easily be proved using similarity but what I want to ask in this question is "Should statements like this, which are assumed to be obvious and trivial be proved before attempting questions like the example I gave and would the solution to this example be rendered as invalid if this statement has not been proved beforehand?"

    Thank You!

    • Rajdeep Sindhu
    • 1,573
    • Not sure I follow the question, but the rule of thumb is to make sure you could spell things out if you had to, but, when possible, spare yourself and the reader as much pain as possible. – pancini Aug 19 '20 at 06:23
    • 1
      Also, I would define $\cos$ and $\sin$ as the horizontal and vertical coordinates of a point on the unit circle. Then there is no reference to right triangles, so no question of well-defined-ness – pancini Aug 19 '20 at 06:24
    • 1
      The problem then, @ElliotG, is that it's by no means obvious how we deal with arbitrary right-angled triangles. As the OP says there is a lot that we treat as axiomatic when we start out, and only later do we see what the minimal assumptions are, and proved that the other things follow. – ancient mathematician Aug 19 '20 at 06:27
    • Exactly @ancientmathematician you understood it perfectly :-) – Rajdeep Sindhu Aug 19 '20 at 06:32
    • 2
      @ElliotG I know about the unit circle definition as well. But, that's not how we define trigonometric ratios (later, functions) in the beginning. That's why I wrote in introductory trigonometry – Rajdeep Sindhu Aug 19 '20 at 06:33
    • @ancientmathematician I think defining them as the values on a circle is much better and you can easily derive the results on right angle triangles from there. –  Aug 19 '20 at 06:41
    • @Elliot G: The OP is not asking how one might better define the trigonometric ratios, but instead the OP is asking something about the specific way the trigonometric ratios are introduced and worked with in the particular textbook the OP is studying from (or had previously studied from). – Dave L. Renfro Aug 19 '20 at 07:31
    • @tomasliam It is not "easy". Either you postulate that translations, rotations, reflections don't change the side ratios; or else you work in coordinate geometry (and of course you've got to prove that you can coordinate the plane which Euclid talks about) and prove these facts. – ancient mathematician Aug 19 '20 at 08:32
    • @DaveL.Renfro It's not just in the specific textbook I used, though. In India, trigonometry is introduced in 10th grade and trig ratios are defined in terms of sides of a right triangle. In 11th grade, radians and unit circles and trigonometric functions (not ratios) are introduced. – Rajdeep Sindhu Aug 19 '20 at 08:48
    • Look, as David L. Renfro pointed out, this isn't really what the OP asked. I am not sure the axioms we are assuming so perhaps you are right and I cannot do this, but I assumed Pythagoras' theorem (which I thought had an elementary proof) and easily showed that two similar right angle triangles have the same side ratios. @ancientmathematician –  Aug 19 '20 at 08:50
    • @tomasliam I don't quite understand all the comments here, to be honest. The thing is, when I learned trigonometry, this was just taken for granted that the sine of an angle is unique and does not depend on the right triangle that you choose (the trig functions have been defined in terms of sides of a right triangle in this context). I just want to ask if this is something that should have been proved beforehand (using similarity) and if the solution (included in my post) is invalid without the proof of this. Does this clarify it? – Rajdeep Sindhu Aug 19 '20 at 08:54
    • @RajdeepSindhu that comment was aimed at ancientmathematician. Sorry, this is sort of a sub-discussion that probably doesn't belong here. I understand your question and my comments aren't really addressing it. –  Aug 19 '20 at 08:58
    • @tomasliam What do you mean 'aimed at ancientmathematician'? I think he understands the question perfectly, like I mentioned in one of the comments... – Rajdeep Sindhu Aug 19 '20 at 09:36
    • I am not saying he doesn't. As I was saying it is a sub-discussion. Read the comments by ancientmathematician and myself. –  Aug 19 '20 at 09:38
    • 1
      In India, trigonometry is introduced in 10th grade --- In most cases I'm familiar with this is true from my experiences also, namely right triangle trigonometry usually comes first. Indeed, at the school level I think right triangle trigonometry should come first. In the U.S., 1-semester college trig. courses sometimes start with the unit circle, but such students have nearly always seen some trig. before (they just didn't learn much of it for various reasons). – Dave L. Renfro Aug 19 '20 at 10:36
    • 1
      just taken for granted that the sine of an angle is unique and does not depend on the right triangle that you choose --- I would be surprised if any trig. text did not point this out. Although I probably have over 30 trig. texts on my bookshelves that I could look at now (from mid 1800s to 1990s), this isn't something I feel is even worth going to the trouble of looking. Besides, I've taught trig. over 30 times between 1983 and 2005 (either as a 1-semester stand-alone course or as part of a precalculus course), and the several texts I've used definitely do this. (continued) – Dave L. Renfro Aug 19 '20 at 10:42
    • 1
      My approach was to remind students of 45-45-90 and 30-60-90 triangle properties, working some of the standard geometry "applied problems" that make use of them, and pointing out the geometry fact that the ratios of corresponding sides of similar triangles are the same (where "similar" is defined by having the same three angles; and mentioning as side comment that for quadrilaterals, defining "similar" as having the same four angles doesn't work). Then I draw (for example) a 20-70-90 triangle and put up decimal approximations for side ratios, saying there are also similar rules for these . . . – Dave L. Renfro Aug 19 '20 at 10:48
    • @DaveL.Renfro Nice comments. I think that these comments would have been pretty appropriate as an answer. I haven't encountered a single book yet which proves that the sine of a given angle is unique and does not depend on the triangle taken into context. Even the textbook that all schools use, published by NCERT (National Council of Education and Research Training) doesn't mention anything like that. – Rajdeep Sindhu Aug 19 '20 at 12:40
    • I don't want to sound rude but I'm pretty sure the percentage of Indian children who actually care about understanding stuff (rather than just "scoring good") with respect to the total number of students who study is an infinitesimal number. So, most kids just don't care because it won't be asked in any exam. – Rajdeep Sindhu Aug 19 '20 at 12:42
    • 1
      See p. 22 of Elementary And Advanced Trigonometry by Kenneth S. Miller for the type of discussion I'm used to seeing in textbooks (e.g. I've taught from two older editions of Barnett's Analytic Trigonometry with Applications). Although Miller's book is for a more advanced treatment (see here for others), the discussion on p. 22 of his book is almost exactly what is in standard school/college level trig. texts I'm used to. – Dave L. Renfro Aug 19 '20 at 14:48

    1 Answers1

    2

    Before you introduce the trigonometric functions the class will deal with congruence and similarity. Congruent triangles have equal sides and equal angles, and similar triangles have equal angles, whereas the sides are scaled by the same factor $>0$. When the pupils accept these facts there is no problem of unicity of $\sin\alpha$ when $0\leq\alpha\leq{\pi\over2}$.

    The main problem of course is the "secret" dependence between side lengths and angles. This dependence is not dealt with by axiomatic euclidean geometry.

    Christian Blatter
    • 232,144
    • As an addendum: your opening statements all follow from the intercept theorem (or Thales' theorem). Depending on your country, this theorem should explicitly be part of your curriculum. – Vercassivelaunos Aug 19 '20 at 07:38